


Next: Experiment 1: Single Model
Up: Multi-Model Estimation and Classification
Previous: Physical Models of Sound
Techniques for estimating parameters using function approximation have
been discussed in previous papers, [4] [5]
[1]. We will summarize this work here.
The basic problem is to find an inverse mapping of a sound-generating
system. A physical model can be thought of as performing a mapping
from parameters to a sound outcome; we wish to map from a sound
intention to the physical parameters. These parameters comprise a
description of the sound. By selecting the correct model and
estimating the parameters we can extract physically meaningful
information from the sounding world.
There are two basic architectures to consider for parameter
estimation; dynamic and static parametric modeling. Dynamic modeling,
[5], needs an explicit time stamp in order to give
instantaneous parameter estimates as a function of time. In dynamic
modeling it is assumed that the parameters vary significantly as a
function of time, thus for each sound a set of time-varying parameters
are extracted.\
One of the major drawbacks of dynamic parameter estimation is that it
explicitly encodes for each moment of a sounds evolution in terms of
articulator activity. Sounds evolve in time even if the parameters are
static, such is the case in physical modeling where a set of
stationary parameters give rise to a complex evolving signal.\
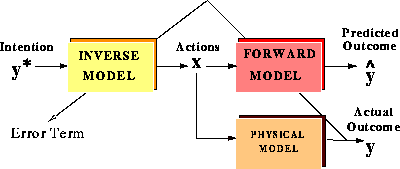
Figure 3: Distal Learning Architecture. A forward model of the physical environment
is used to constrain the learning of an inverse model. The parameters that the
inverse model estimates are then passed through to the physical environment and the
environment performance error is used to fine-tune the inverse estimator.
We chose to implement a static parameter estimator whose input is a
dynamic sound representation and whose output is a set of stationary
parameters; see Figure 3. The justification for this
approach is that there are far fewer parameters that vary than those
that are static. Much of the variation in musical instrument
articulators is in expressive control; such as in the use of
vibrato. These dynamic parameters often operate at very low frequency
and can be described as a simple function of time. Thus, even dynamic
parameters can be reduced to a static description if an appropriate
function generator is selected.\
Static parameter estimators are more robust, simpler to implement and
require less training data than dynamic estimators. We also believe
that they form a better model of perception than dynamic estimators.



Next: Experiment 1: Single Model
Up: Multi-Model Estimation and Classification
Previous: Physical Models of Sound
Michael Casey
Fri Mar 22 15:49:22 EST 1996
