| The "Keith Haring" Look. | Glowing Books |

|

|
| The "Keith Haring" Look. | Glowing Books |

|

|
Color constancy is a psychophysical phenomenon that accounts for the ability of humans to accurately perceive the "color" of an object under different lighting conditions. The lighting, or illumination, may vary both over a viewed scene (indeed, constant illumination over scene is almost never encountered in real life), and over time. For example, the spectral content ("color") of sunlight varies greatly through the day and with weather conditions. Artificial light sources vary greatly from one to another. Yet the colors we perceive (within limits) remain the same.
A discussion of of the color constancy problem, and previously suggested techniques for solving it is provided in an accompanying document.
These are a number of simple experiments applying different color constancy algorithms to a common set of test images. The goal was to find a simple method of "correcting the color" of a video sequence digitized by a computer. Ideally this would provide an image whose pixel values represented the scene contents viewed under a "standard white illuminant".
 I started by gathering some experimental data.
While much of the research into color constancy has attempted to constrain
the experimental variables by using synthetic data, my goals required that
any solution proposed work well with real data. A video camera was used
to record several similar scenes under three different "illuminant" conditions.
I started by gathering some experimental data.
While much of the research into color constancy has attempted to constrain
the experimental variables by using synthetic data, my goals required that
any solution proposed work well with real data. A video camera was used
to record several similar scenes under three different "illuminant" conditions.
One restriction on the test images (which required a regathering of data) was a need for high spatial frequencies in the resulting images. One particular algorithm being tested requires the use of good luminance edge information.
The first approach tried was to apply a global von Kries adaptation (global in that the correction factors are constant for the entire image). One implicit assumption of global adaptation is that the scene is illuminated by a single light source, and that the illumination is primarily direct (i.e. not "colored" by reflecting off a non-white surfaces.) One of two different assumptions about the nature of the surfaces in the scene are often used to constrain the problem of estimating the spectral content ("color") of the illuminant:
These assumptions are not met in many real scenes, and the results of directly applying the assumptions shows this. The poor results obtained quickly led me to investigate more complex techniques, such as Hurlbert Regularization.
In the interest of meeting my goals, however, I ended up returning to a global adaptation approach. I suggest a hybrid, Light Gray World approach, which performs well better than either the white world or gray world approaches alone.
After doing some searching of recent research on the subject of color constancy, I decided to implement an approach proposed by Dr. Anya Hurlbert in her doctoral dissertation, "The Computation of Color", which contains elements of both Land's "Retinex" theory and Horn's solution. See the accompanying text for an introduction to her work. Her approach basically attempts to compute a "color" value which corresponds to that perceived by a human observer.
Some of the best results seem to be in Test 6 or Test 7. I also tested the algorithm on a pair of Koffka Ring test images, for which it gave a response similar to that of the human visual system.
My implementation of her color constancy algorithm is shown in the following block diagram. It consists of two major components, the lightness calculation, which applies a linear filter independently to each sensor input to "remove" the illuminant, and a relaxation step, which enforces a constraint that regions (bounded by luminance edges) should have a similar perceived color. A spectral normalization step assumes a gray world and biases the perceived lightness accordingly, before the relaxation is performed. In order to produce viewable images, the calculated chroma values are remixed with the original luminance signal.
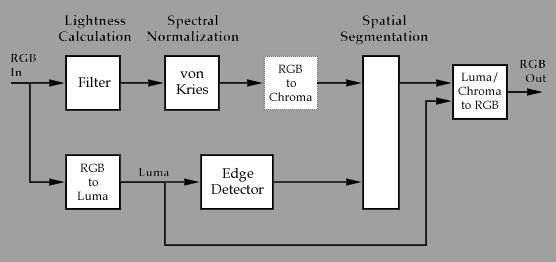
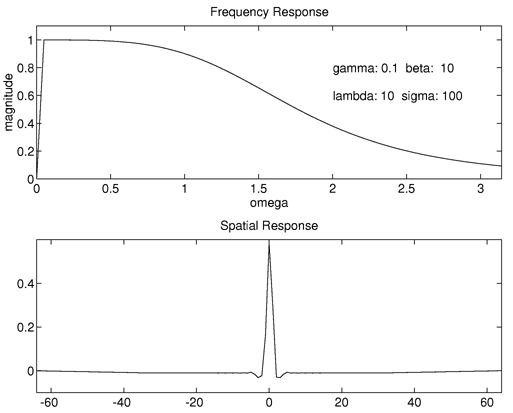
A lot of time was spent experimenting with different parameters for the lightness calculation step. Hurlbert provides an equation for the frequency response of the optimum lightness filter given four parameters:
A fifth parameter is filter length, which was fixed at 128 taps for these experiments (the images are 320x240). Earlier experiments (not retained, except for the Haring look-alike) showed the folly of using smaller filter sizes.
This Matlab procedure was used to compute the different regularization filters used in this experiment. A typical filter is shown in the below figure. The top plot is the 1D frequency response of the filter, and the bottom trace shows a 1D spatial response.
The relaxation step was implemented as briefly described in her dissertation, and consisted of an iterative implementation of a two-dimensional diffusion equation, modified to prevent diffusion accross edges. The number of iterations to perform is the sole parameter of the relaxation step.
Here are some of the more recent results, using different filter parameters:
| Exp. | Gamma | Beta | Sigma | Lambda | Num. Iterations | Notes |
|---|---|---|---|---|---|---|
| Test 8A | 0.1 | 10 | 100 | 10 | 300 | |
| Test 8 | 0.1 | 10 | 20 | 10 | 200 | |
| Test 7A | 0.1 | 10 | 100 | 10 | 150 | RGB relaxation process |
| Test 7 | 0.1 | 10 | 100 | 10 | 200 | |
| Test 6 | 0.1 | 10 | 100 | 10 | 50 | |
| Test 5 | 0.1 | 5 | 20 | 10 | 200 | |
| Test 4 | 1 | 0.3 | 20 | 10 | 80 | |
| Test 3 | 1 | 0.3 | 20 | 10 | 30 |
One of the question encountered when implementing this system was the color space in which to perform the chroma relaxation. While all of the above experiments performed relaxation in a chromaticity space (normalized red vs. normalized blue), in test 7A I duplicated test 7, performing the chroma relaxation in RGB space instead. A side-by-side comparison is available.
While the Hurlbert regularization approach has many problems, it does show promise. It does compute "colors" which seems to match those perceived by humans. On the other hand, the relaxation step is unwieldy, and seems to be the more error-prone part of the process.
This experiment started out using a variety of tools (the garden dat utilities and a hand calculator, for example) but ended up being supported completely by a neat and nifty image manipulation language, Isis, being developed by the TVOT group here at the MIT Media Lab. Isis is a variant of Scheme, designed to support synchronized multimedia processing and presentation, which proved easy to use.
Completely implementing the regularization in Isis required that additional language primitives be written (mainly in C.) These included functions for computing image statistics as well as color transformations and a dedicated function to perform the chroma relaxation for Hurlbert regularization.