One of the earliest color constancy algorithms was von Kries
adaptation [vK78] [WB82]. It uses a linear scaling
independently, applied independently to each receptor channel, to
adapt to changing global lighting conditions. I will use
to denote the energy integrated by the sensor for the
spectral region, 
to denote the illuminant
energy in the same spectral regions, and 
to represent the
body reflectance of the surface being viewed. A simple reflection
model provides:
The correction factors, 
, are then calculated as:
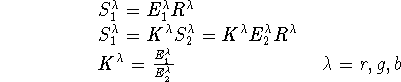
The simplicity of this approach both makes it appealing, and is it's fatal flaw. Nonetheless, this solution is returned to by many algorithms.
A basic problem is introduced along with this first algorithm: that of estimating the chromaticity in the received stimulus due to an object's illumination in order to cancel it out. The two most straightforward methods for global illuminant estimation and correction are average-to-gray and normalize-to-white. The gray world assumption is that the average of a surface reflectances in a scene is gray. The white world assumption, on the other hand is that each scene contains a object with a white reflectance. While simple application of these assumptions provides little constancy (see Section 4), one of these two assumptions is utilized by all of the lightness algorithms. A second, less scknowledged (but just as common) assumption is that of a single illuminant (in the spectral, not spatial, sense) [Hur89].
Helson and Judd performed many experiments [HJ36] [Hel38] [Jud40] to establish the parameters of color constancy in the human visual system. The model they proposed correctly estimates perceived color under a variety of conditions. They did not propose a theory of color vision, instead providing an empirical model of how color constancy is vioslated as the illuminant and background change.
The first effect they modeled was to ``discount the illuminant''. This consisted of calculating the stimulus of a (possibly hypothetical) white patch, and using this to determine the color of other patches. This white ( denoted by N ) is generated by interpolating between the ``average'' color in the whole visual field ( G ) and a standard daylight white ( W ) :
Several additional modifications are added to this to account for secondary effects, making the model non-linear. A quick intro to their work is found in Marr (p.252) [Mar82], and Section 1.3 introduces a color correction algorithm based on their work.
Land and McCann [LM71] proposed a ``Retinex'' theory of color vision which is notable for incorporating the effects of edges into a model of color vision. Unfortunately, while working well under a limited set of conditions, the ``retinex'' theory fails under many common conditions. A detailed introduction to this original retinex theory relevant to this topic may be found in the Appendix of Hardin's ``Color''[Har93], or in Marr [Mar82].
Edwin Land later presented a refined version of the Retinex theory
Richards & Parks [RP71] propose a model for color constancy which introduces two modifications to the von Kries model. The first modification regards how the global illuminant is calculated and accounted for. They propose, in a manner similar to Helson & Judd [Jud40], to estimate the illuminant as being linearly interpolated between the illuminant and a ``neutral white''. They chose CIE coordinates x = 1/3, y = 1/3 for ``neutral white'', and the effective achromatic point to be 70the neutral and the measured illuminant:
an induced contrast effect is nonlinear correction corrsponding to Helson In the second stage, a local applied. A simpler, single stage, model was later proposed [Ric72].
``The Computation of Color'' [Hur89] is a PhD thesis out of the Brain & Cognitive Science Dept. at MIT, by Anya Hurlbert under the tutelage of T. Poggio. In addition at a good introduction to algorithms for computing color, its major contributions are: