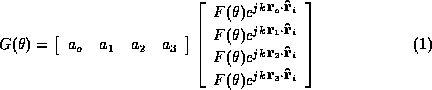In this section we describe a fixed beamformer algorithm and the
different microphone arrangements that can be used with it.
The geometry of the microphone array is represented
by the set of vectors 
which describe the position of each
microphone n relative to some reference point (e.g., the center of
the array), see Figure 3. The array is steered
to maximize the response to plane waves coming from the direction
of frequency 
. Then, for a plane wave incident
from the direction 
, at angle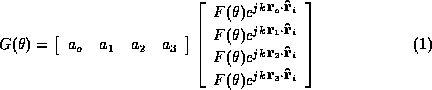 
, the gain is:
where 
, 
is the gain pattern of each individual
microphone, and k 
is the wave number of the incident
plane wave. 
is the wave number corresponding to the frequency
of the incident plane wave. Note that there is also a
dependence for F and G, but since we are only interested in
steering in one dimension, we have omitted this factor. This
expression can be written more compactly as:
where 
represents the microphone weights and 
is the set
of transfer functions between each microphone and the reference point.
In the formulation above, a maxima is created in the gain pattern at
the steering angle for the expected frequency, since 
and the phase terms in and cancel each other. Note, however, that this is not the only set
of weights that can be used for . For example, Stadler and Rabinowitz
present a method of obtaining the weights with a parameter
that arbitrates high directivity and uncorrelated noise gain
[7]. This method, when used to obtain maximum directivity, yields gain
patterns that are slightly more directional than the basic weights
described above.
The standard performance metric for the directionality of a fixed array is the directivity index which is shown in Equation 3, [7]. The directivity index is the ratio of the array output power due to sound arriving from the far field in the target direction, , to the output power due to sound arriving from all other directions in a spherically isotropic noise field,
The directivity index thus formulated is a narrow-band performance metric; it is dependent on frequency but the frequency terms are omitted from Equation 3 for simplicity of notation. In order to assess an array for use in speech enhancement a broad-band performance metric must be used.\
One such metric is the intelligibility-weighted directivity index [7] in which the directivity index is weighted by a set of frequency-dependent coefficients provided by the ANSI standard for the speech articulation index [1]. This metric weights the directivity index in fourteen one-third-octave bands spanning 180 to 4500 Hz [7].
