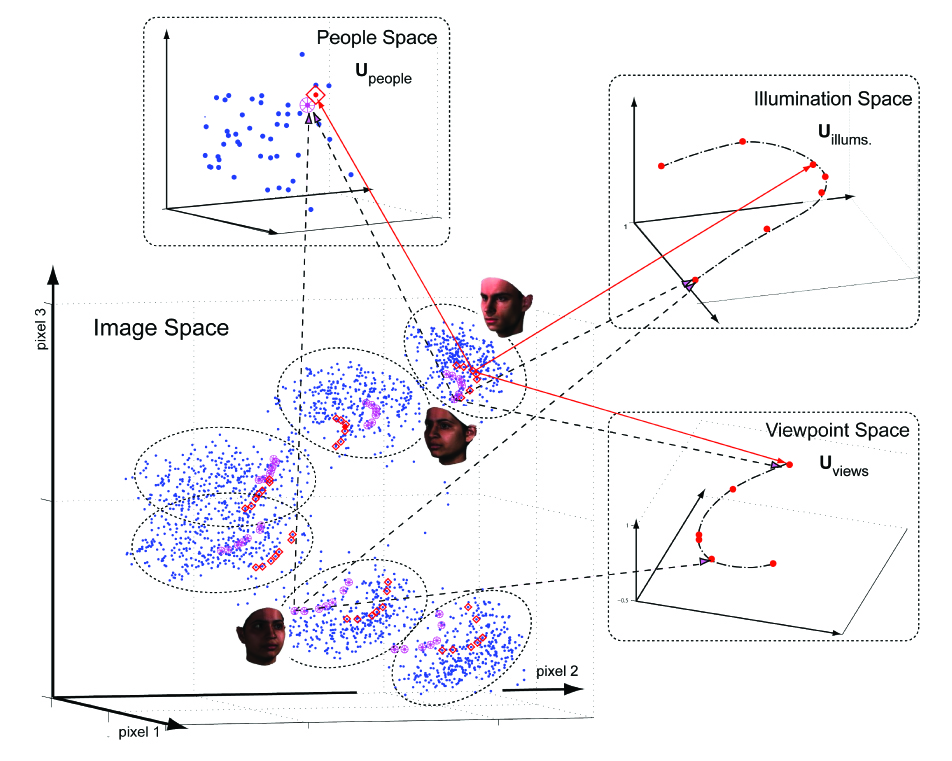
Generalizing concepts from linear (matrix) algebra, we define the
mode-n identity tensor and the mode-n pseudo-inverse tensor and we
employ them to develop a multilinear projection algorithm in order to performing recognition in the tensor algebraic framework. Multilinear projection simultaneously
projects an unlabeled test image into multiple constituent
mode spaces, associated with image formation, in order to infer the mode labels. Multilinear
projection is applied to unconstrained facial image recognition, where
the mode labels are person identity, viewpoint, illumination, etc.
- "Multilinear Projection for Face Recognition via Canonical Decomposition ",
M.A.O. Vasilescu, In Proc. Face and Gesture Conf. (FG'11), 476-483.
- "Multilinear Projection for Face Recognition via Rank-1 Analysis ",
M.A.O. Vasilescu, CVPR, IEEE Computer Society and IEEE Biometrics Council
Workshop on Biometrics, June 18, 2010.
-
"Multilinear Projection for Appearance-Based Recognition in the Tensor Framework", M.A.O. Vasilescu and D. Terzopoulos,
Proc. Eleventh IEEE International Conf. on Computer Vision (ICCV'07), Rio de Janeiro, Brazil, October, 2007, 1-8.
Paper (1,027 KB - .pdf)
-
“Multilinear Independent Components Analysis and Multilinear
Projection Operator for Face Recognition”, M.A.O. Vasilescu, D. Terzopoulos, in
Workshop on Tensor Decompositions and Applications, CIRM, Luminy, Marseille,
France, August 2005.
Independent Component Analysis (ICA)
minimizes the statistical dependence of the representational
components of a training image ensemble, but it cannot distinguish
between the different factors related to scene structure, illumination
and imaging, which are inherent to image formation. We introduce a
nonlinear, multifactor model that generalizes ICA. A Multilinear
ICA (MICA) model of image ensembles learns the statistically
independent components of multiple factors. Whereas ICA employs linear
(matrix) algebra, MICA exploits multilinear (tensor) algebra. In the
context of facial image ensembles, we demonstrate that the statistical
regularities learned by MICA capture information that improves
automatic face recognition.
-
"Multilinear (Tensor) ICA and Dimensionality Reduction", M.A.O. Vasilescu, D. Terzopoulos, Proc. 7th International
Conference on Independent Component Analysis and Signal Separation (ICA07), London, UK, September, 2007. In
Lecture Notes in Computer Science, 4666, Springer-Verlag, New York, 2007, 818–826.
-
"Multilinear Independent Components Analysis", M. A. O. Vasilescu and D. Terzopoulos, Proc. Computer Vision and Pattern
Recognition Conf. (CVPR '05), San Diego, CA, June 2005, vol.1, 547-553.
Paper (1,027 KB - .pdf)
-
"Multilinear Independent Component Analysis", M. A. O. Vasilescu and D. Terzopoulos, Learning 2004 Snowbird, UT, April, 2004.
An essential goal of computer graphics is photorealistic rendering,
the synthesis of images of virtual scenes visually indistinguishable
from those of natural scenes. Unlike traditional model-based
rendering, whose photorealism is limited by model complexity, an
emerging and highly active research area known as {\it image-based
rendering} eschews complex geometric models in favor of representing
scenes by ensembles of example images. These are used to render novel
photoreal images of the scene from arbitrary viewpoints and
illuminations, thus decoupling rendering from scene complexity. The
challenge is to develop structured representations in high-dimensional
image spaces that are rich enough to capture important information for
synthesizing new images, including details such as self-occlusion,
self-shadowing, interreflections, and subsurface scattering.
TensorTextures, a new image-based texture
mapping technique, is a rich generative model that, from a sparse set
of example images, learns the interaction between viewpoint,
illumination, and geometry that determines detailed surface
appearance. Mathematically, TensorTextures is a nonlinear model of texture
image ensembles that exploits tensor algebra and the N-mode SVD to
learn a representation of the bidirectional texture function (BTF) in
which the multiple constituent factors, or modes---viewpoints and
illuminations---are disentangled and represented
explicitly.
-
"TensorTextures: Multilinear Image-Based Rendering", M. A. O. Vasilescu and D. Terzopoulos, Proc. ACM SIGGRAPH 2004 Conference Los Angeles, CA, August, 2004, in Computer Graphics Proceedings, Annual Conference Series, 2004, 336-342.
Paper (5,104 KB - .pdf)
Animations:
- TensorTextures -
AVI
(54,225 KB)
- TensorTextures Strategic Dimensionality Reduction -
AVI
(19,650 KB)
- TensorTextures Trailer -
AVI
(17,605 KB)
-
"TensorTextures", M. A. O. Vasilescu and D. Terzopoulos, Sketches
and Applications SIGGRAPH 2003 San Diego, CA, July, 2003.
Sketch (6MB - .pdf)
The goal of machine vision is automated
image understanding and object recognition by a computer. Recent
events have redoubled interest in biometrics and the application of
computer vision technologies to non-obtrusive identification,
surveillance, tracking, etc. Face recognition is a difficult problem
for computers. This is due largely to the fact that images are the
composite consequence of multiple factors relating to scene structure
(i.e., the location and shapes of visible objects), illumination
(i.e., the location and types of light sources), and imaging (i.e.,
viewpoint, viewing direction and camera characteristics). Multiple
factors can confuse and mislead an automated recognition system. In
addressing this problem, we take advantage of the assets of
multilinear algebra, the algebra of higher-order tensors, to obtain a
parsimonious representation that separates the various constituent
factors. Our new representation of facial images, called TensorFaces,
leads to improved recognition algorithms for use in the aforementioned
applications.
-
"Tensor subspace Analysis for Viewpoint Recognition", T. Ivanov, L. Mathies, M.A.O. Vasilescu, ICCV, 2nd IEEE International
Workshop on Subspace Methods, September, 2009.
-
"Multilinear Subspace Analysis for Image Ensembles,'' M. A. O. Vasilescu, D.
Terzopoulos, Proc. Computer Vision and Pattern
Recognition Conf. (CVPR '03), Vol.2, Madison, WI, June, 2003, 93-99.
Paper (1,657KB - .pdf)
-
"Multilinear Image Analysis for Facial Recognition,'' M. A. O. Vasilescu, D.
Terzopoulos, Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 2, Quebec City, Canada, Aug, 2002, 511-514.
Paper (439KB
- .pdf)
-
"Multilinear Analysis of Image Ensembles: TensorFaces," M. A. O.
Vasilescu, D. Terzopoulos, Proc. 7th European Conference on
Computer Vision (ECCV'02), Copenhagen, Denmark, May, 2002, in Computer
Vision -- ECCV 2002, Lecture Notes in Computer Science, Vol. 2350,
A. Heyden et al. (Eds.), Springer-Verlag, Berlin, 2002, 447-460.
Full Article in PDF
(882KB)
Given motion capture samples of Charlie Chaplin's walk, is it possible
to sysignatures, do people have characteristic motion signatures that
individualize their movements? If so, can these signatures be
extracted from example motions? Furthermore, can extracted signatures
be used to recognize, say, a particular individual's walk subsequent
to observing examples of other movements produced by this individual?
We have developed an algorithm that extracts motion signatures and
uses them in the animation of graphical characters. The mathematical
basis of our algorithm is a statistical numerical technique known as
n-mode analysis. For example, given a corpus of walking, stair
ascending, and stair descending motion data collected over a group of
subjects, plus a sample walking motion for a new subject, our
algorithm can synthesize never before seen ascending and descending
motions in the distinctive style of this new individual.
-
"Human Motion Signatures: Analysis, Synthesis, Recognition," M. A. O. Vasilescu
Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 3, Quebec City, Canada, Aug, 2002, 456-460.
Paper
(439KB - .pdf)
-
"An Algorithm for Extracting Human Motion Signatures", M. A. O. Vasilescu, Computer Vision and Pattern Recognition
CVPR 2001 Technical Sketches, Lihue, HI, December, 2001.
-
"Human Motion Signatures for Character Animations", M. A. O. Vasilescu, Sketch and Applications SIGGRAPH 2001 Los Angeles,
CA, August, 2001.
Sketch (141KB - .pdf)
-
"Recognition Action Events from Multiple View Points," Tanveer Sayed-Mahmood, Alex
Vasilescu, Saratendu Sethi, in IEEE Workshop
on Detection and Recognition of Events in Video, International
Conference on Computer Vision (ICCV 2001), Vancuver , Canada, July 8,
2001, 64-72.
Adaptive mesh models for the nonuniform sampling and reconstruction of
visual data. Adaptive meshes are dynamic models assembled from nodal
masses connected by adjustable springs. Acting as mobile sampling
sites, the nodes observe interesting properties of the input data,
such as intensities, depths, gradients, and curvatures. The springs
automatically adjust their stiffnesses based on the locally sampled
information in order to concentrate nodes near rapid variations in the
input data. The representational power of an adaptive mesh is
enhanced by its ability to optimally distribute the available degrees
of freedom of the reconstructed model in accordance with the local
complexity of the data.
We developed open adaptive mesh and closed adaptive shell surfaces based
on triangular or rectangular elements. We propose techniques for
hierarchically subdividing polygonal elements in adaptive meshes and
shells. We also devise a discontinuity detection and preservation
algorithm suitable for the model. Finally, motivated by (nonlinear,
continuous dynamics, discrete observation) Kalman filtering theory, we
generalize our model to the dynamic recursive estimation of nonrigidly
moving surfaces.
-
"Adaptive meshes and shells: Irregular triangulation,
discontinuities, and hierarchical subdivision," M. Vasilescu,
D. Terzopoulos, in Proc. Computer Vision and Pattern
Recognition Conf. (CVPR '92), Champaign , IL, June, 1992, pages 829 -
832.
Paper (652KB - .pdf)
-
"Sampling and Reconstruction with Adaptive Meshes," D. Terzopoulos, M.
Vasilescu, in Proc. Computer Vision and Pattern
Recognition Conf. (CVPR '91), Lahaina, HI, June, 1991, pages 70 - 75.
Paper (438KB - .pdf)
|
|
