In order to evaluate the generalization capabilities of each of the inverse modeling techniques we constructed a novel data set comprising target sounds that required parameter values that were not in the original training set but that were generalized as a result of the learning. We produced a new set of waveforms using the D string on the violin with stop positions that were in quarter-tones with the training set. The frequencies available at a quarter-tone resolution we were limited by:
which gave n = 69. Therefore
( 
). So we had to limit the testing set to 14 waveforms
computed in the range D4 - .
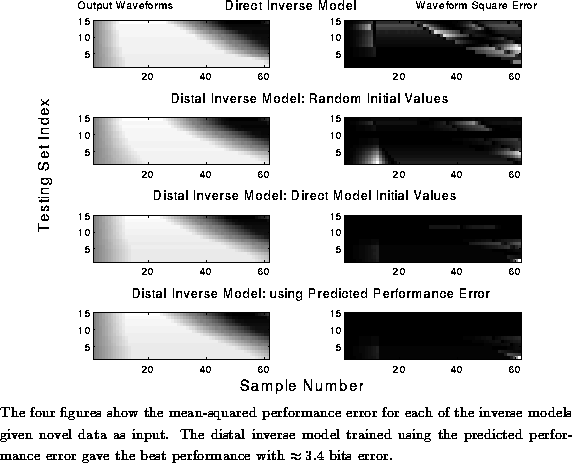
Figure: Mean Performance of the Inverse Models: Novel Data
\
Figures 
and show the
distribution of errors in the output of each of the inverse models.
The inverse model with the best overall performance on the novel data
was the model trained using the predicted performance
error. The mean-squared performance error for this model was
giving an error of bits. The accuracy is better than for the original
training data because we were testing the model in a small range of
the problem space, due to the limited frequency resolution of the
physical model. The results show that the generalization capabilities
of distal inverse models are good for the given problem domain.
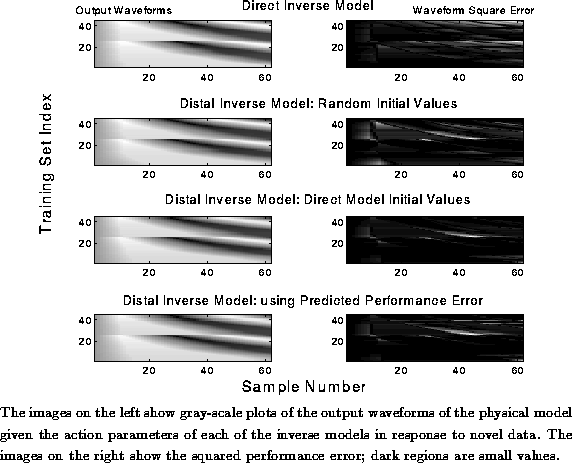
Figure: Performance Outcomes of the Inverse Models: Novel Data
\
