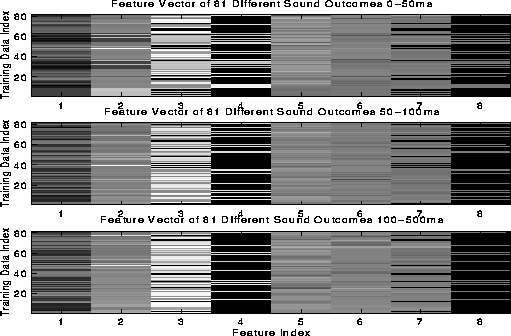
Figure 1: Feature vectors for 81 sounds, the features are extracted for three time intervals; 0-50ms, 50-100ms and 100-500ms.
The representation we chose comprised temporal slices of evolving spectral formants. The center frequencies and magnitudes of up to four formants were used. The feature vector comprised three sets of formants recorded at three fixed times after the onset of the sound. The first and second were split between the first 100ms of the sound. The initial 50ms being encoded in the first and the remaining 50ms in the second. This ensured that a lot of information was retained about the evolution of the attack portion of the signal. The remaining vector encoded the formant center frequencies and magnitudes of the next 400ms of the sound; typically the time when the sound reaches "steady state". A recursive estimator was used to compute the filter coefficients to an all-pole model, the roots to the resulting polynomial in Z were calculated using the Laguer root finding method. Noise residual estimates were also used since the recursive estimator estimates simultaneously for additive noise and pole coefficients. Figure 1 shows an image map of the sound feature representation.

Figure 1: Feature vectors for 81 sounds, the features are extracted
for three time intervals; 0-50ms, 50-100ms and 100-500ms.
This representation had a number of advantages over the other representations: a) It is not dependent on the fundamental frequency of the sound. The All-Pole model extracts the formant structure of the sound. b) Two thirds of the representation are used for the attack and the other third for the steady state component. c) The representation encodes formant center frequency, magnitude and an estimated noise component from the recursive estimator. d) We only need a vector of twenty seven numbers to represent an entire dynamically-evolving sound.
Using these formant-based spectro-temporal vectors as our representation the next step was to acquire function approximations of physical sound-generating systems. We first discuss physical models of sound and then describe function approximation techniques for acquiring cognitive models of such systems.