One requirement of both Extended Kalman filtering and the
Levenberg-Marquardt nonlinear minimization algorithm is that the first
partial derivative of each measured value relative to each state
variable be calculated:
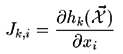
Where x are the components of the state vector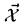 
, i.e. x1 is Tx,
x7 is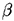 
, etc...
In the case of the Levenberg-Marquardt algorithm, the strict formulation also requires the calculation of the second derivative. If the data being fitted is noisy the effects of the second derivative may be deleterious, and the Hessian (or curvature) matrix is approximated by multiple of first partial derivatives. (For a better overview, see p.682 of Numerical Recipes.)
The Jacobian equations use notation introduced elsewhere for the components of the rotation matrix. In particular, the use of a quaternion representation affects the Jacobian, since the chain rule must be used to relate the incremental angles in the state vector to the components of the rotation matrix.
Other intermediate values used to simplify the Jacobian definition are:
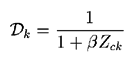
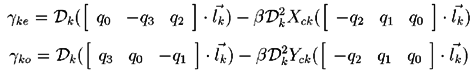
The combined nature of the measurement vector results in the Jacobian having two forms. This first set of equations is for the horizontal measurements (k even) :
The second set of equations applies for vertical measurements (k odd) :
The source code that evaluates the above equations for a given state vector can be found in kalman_camera.c for the EKF and eval_camera.c for the Levenberg-Marquardt method.