

The motion models typically used are simplistic and linear. If the camera motion is small relative to the timestep of the estimation process, this is a reasonable assumption. Specifically, we don't model translational velocity or acceleration, only position. The motion is maintained as the global translational and rotational change since the beginning the estimation.
The representation of rotation is slightly more complex. Since the algorithms being considered require the taking the derivative, much of the current literature strongly recommends avoiding the simplest representation, that of Euler angles (rotational angle around the three cartesian coordinate axes.) Instead, a quaternion representation is used. But given the nature of a quaternion representation, which uses four variables to represent a value with three degrees of freedom, direct estimation is not recommended.
The solution is to store the global rotation at a particular time as
a quaternion, but to estimate an incremental Euler angle relative to the
current rotation. At each step, the global rotation quaternion is updated
using the estimate of incremental rotation.
In any case, a rotation matrix R representing the global
rotation is generated. The components of the rotation matrix are
identified variously as follows :
Although some of the examples in literature
(Broida90,
Kumar89)
directly calculated higher derivatives of motion, by including both
position and translational velocity, rotation and rotational velocity in
the state being estimated, I chose the simpler system model used by
Azarbayejani94 (but not his
structure representation) The system state vector being estimated is
then :
The first six parameters represent the camera translation and incremental
rotation, the seventh is a camera parameter, and the remainder represent
the positions of the feature points in the (arbitrarily scaled) globally frame
of reference.
Each feature point is represented by three points, as opposed to
the single state variable per feature point proposed by Azarbayejani94. Although a
convincing argument is made in their paper that the location of the
feature points in the global space is constrained by the measured
location in the image plane, plus one "hidden state" variable corresponding to
the distance from the image plane, the linearization of the measurement
transformation requires the global X and Y location.
Calculating these from the one state variable and any one measurement (say
the previous one) isn't a good idea due to noisy measurement, requiring
that an estimate of the feature points global X and Y location
be kept separate from the actual state vector.
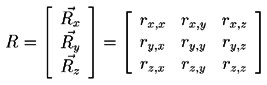
![X = [Tx Ty Tz wx wy wz B X0 Y0 Z0...Xn Yn Zn]](eqn2m.gif)
Jump back to my NMM index page
wad@media.mit.edu