Laser cavity simulations

These demos are inspired by one of the Project Euler problems, which involves a a perfectly reflective cavity in two dimensions, described by an ellipse with equation 4x²+y²=100, and with a pinhole removed at the top between x=-0.01 and x=0.01. A laser enters the cavity and hits a given initial reflection point: the problem is to determine how many times the beam is reflected before it finds the pinhole and exits the cavity again.

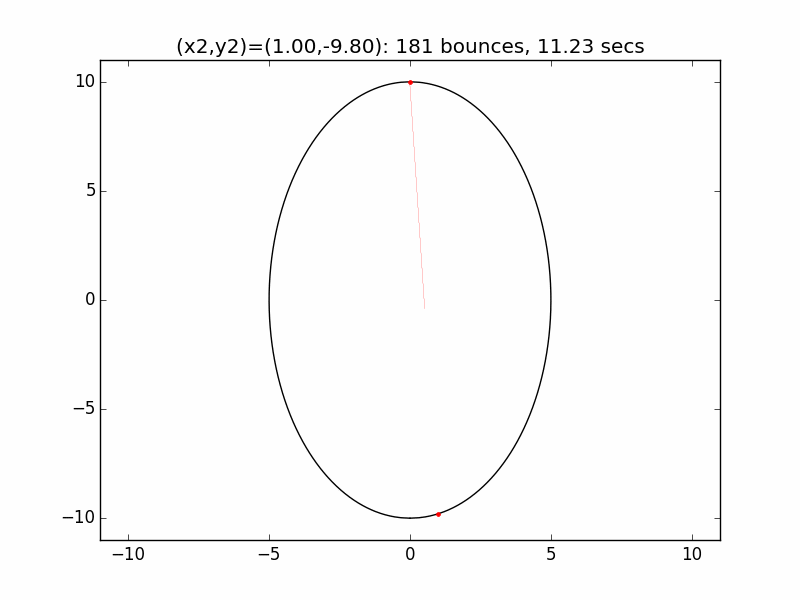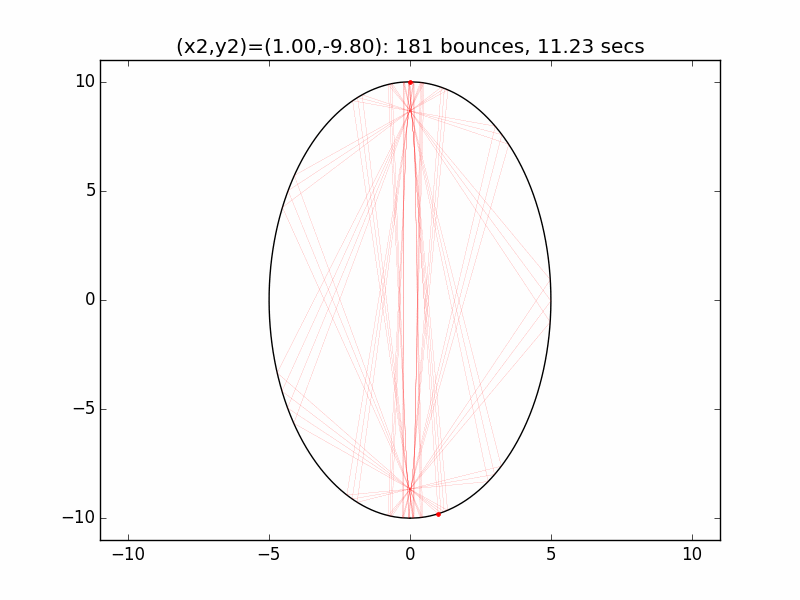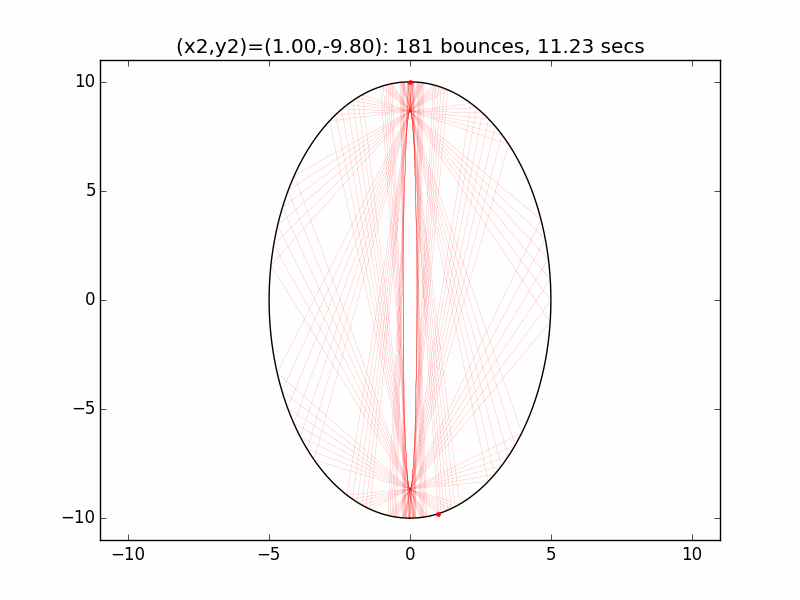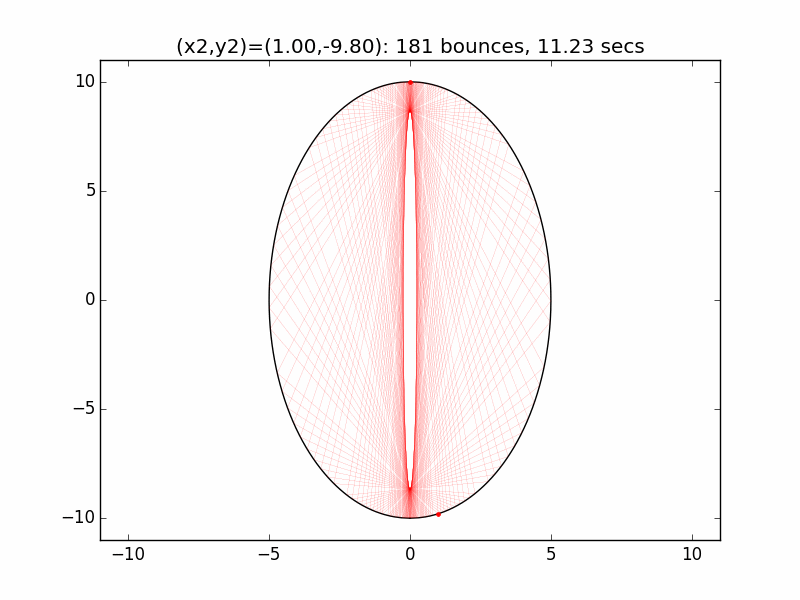
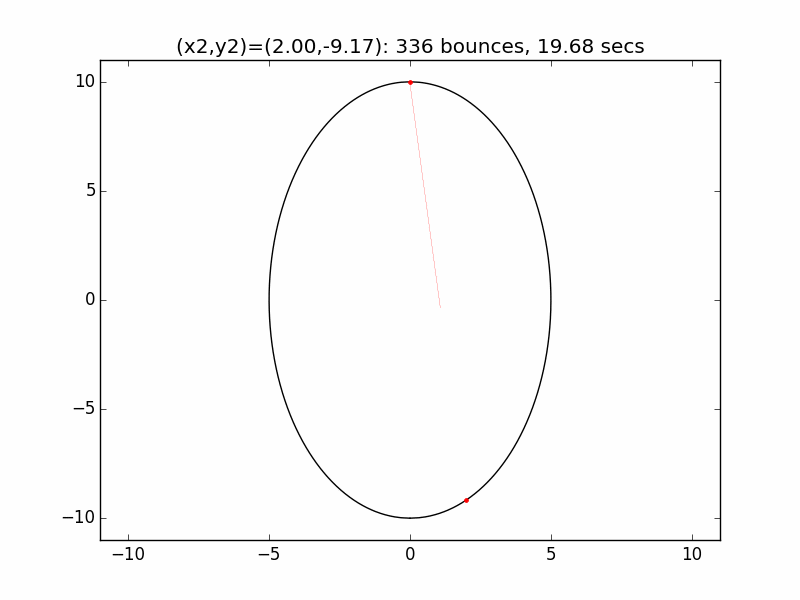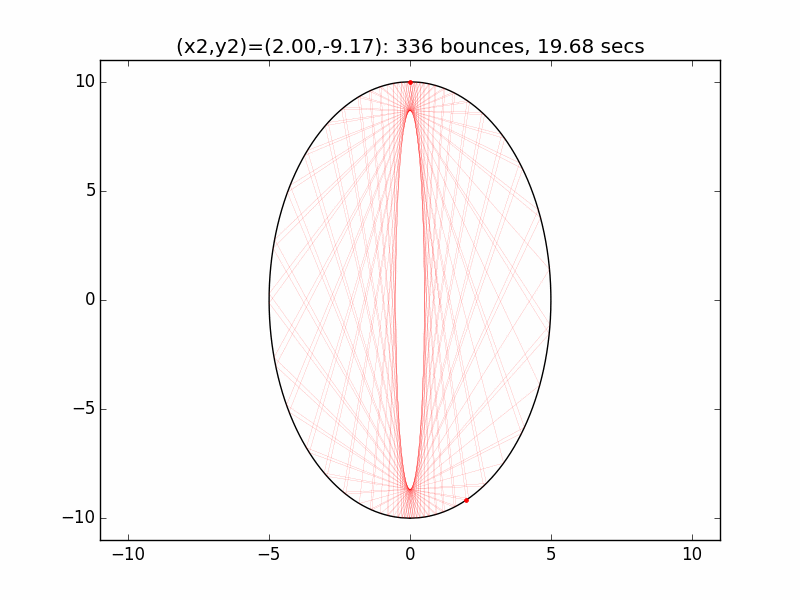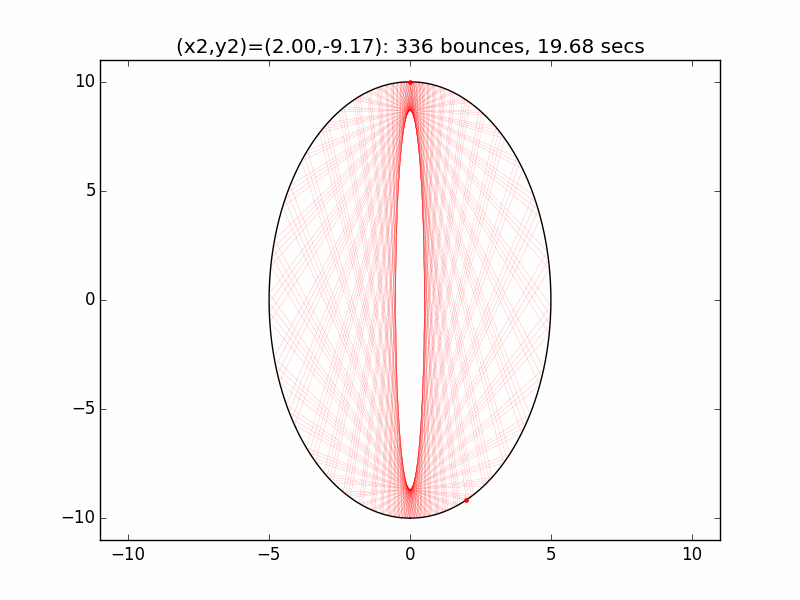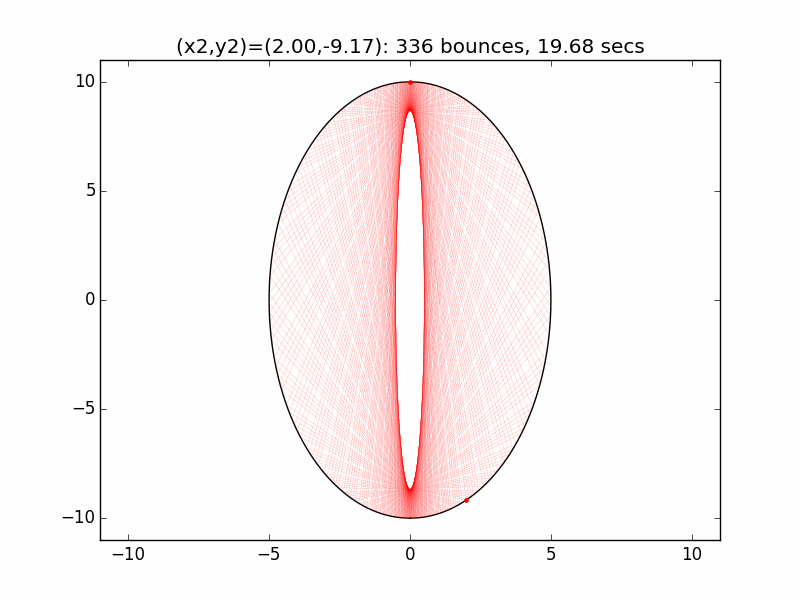
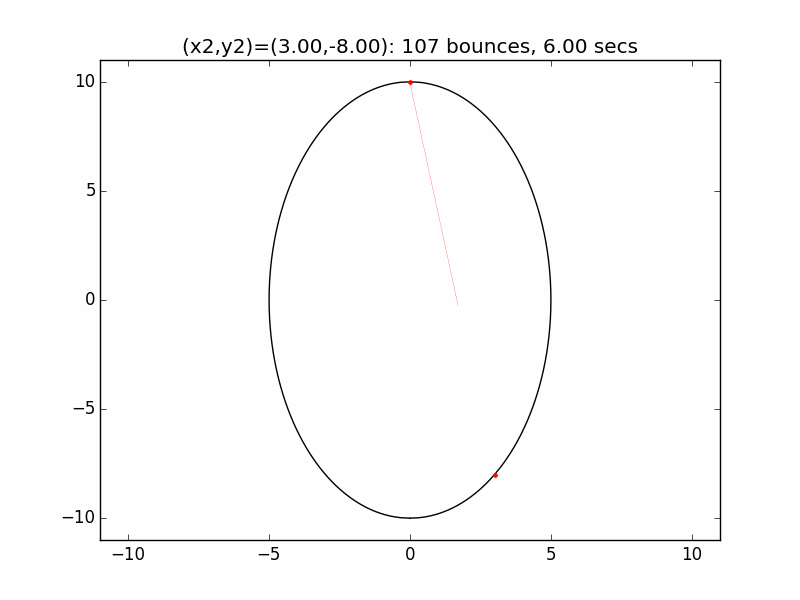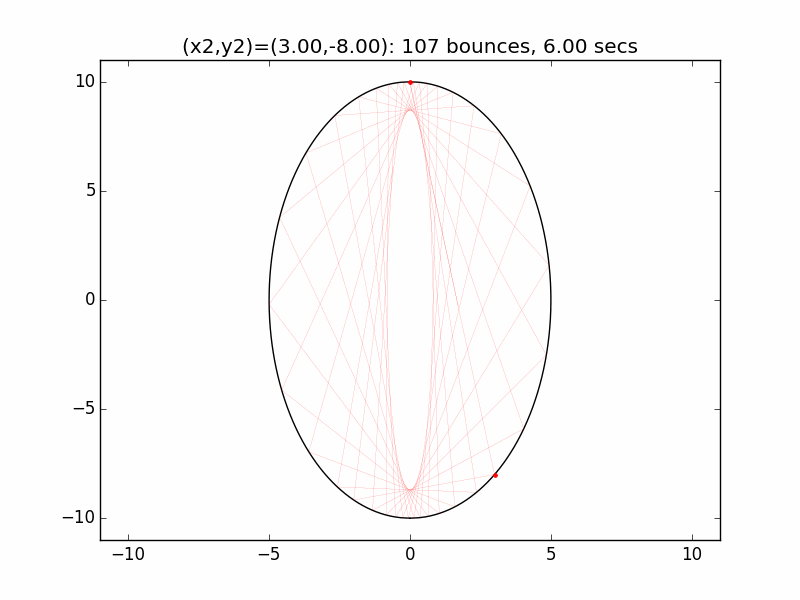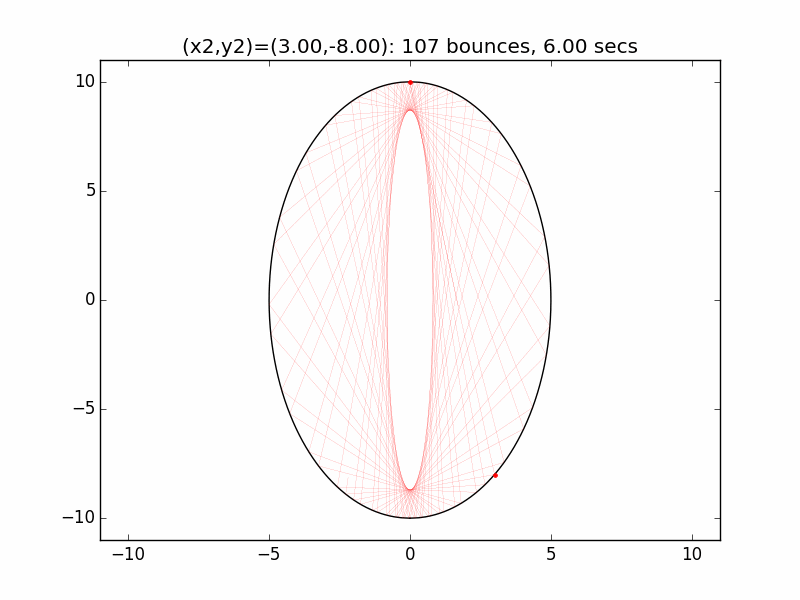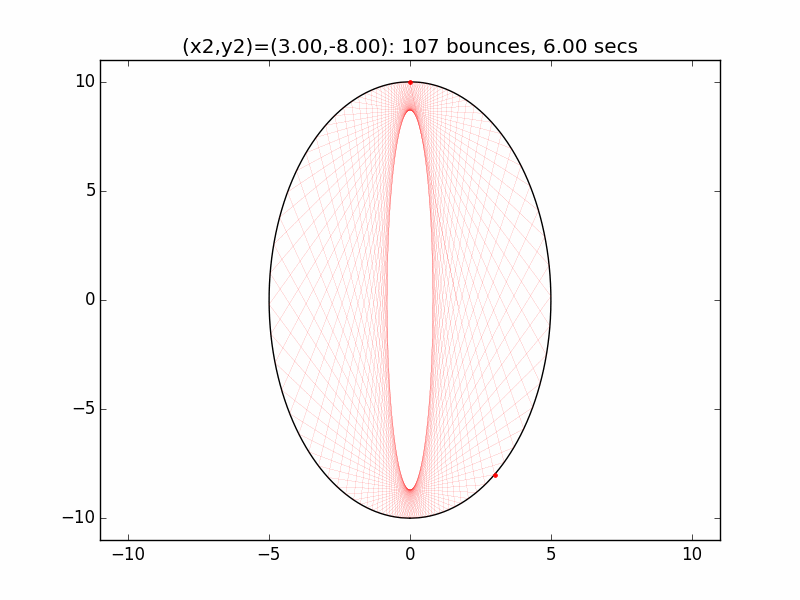
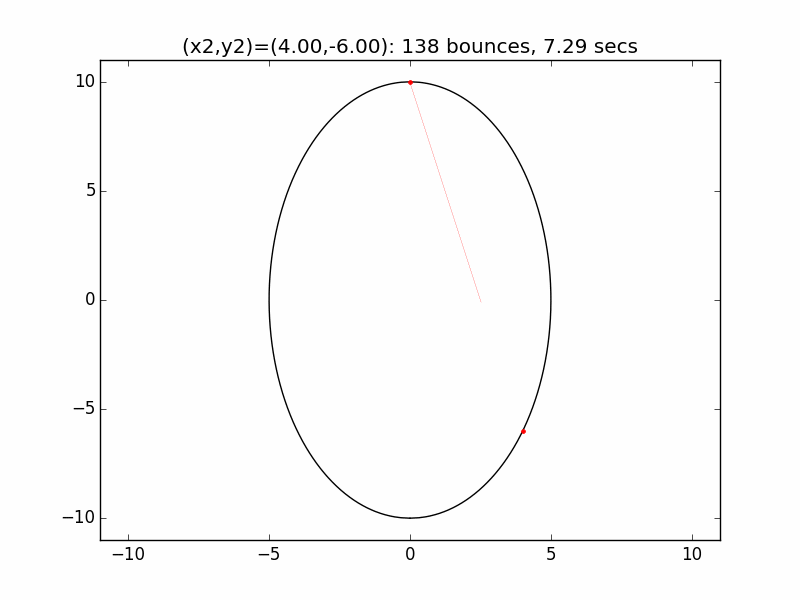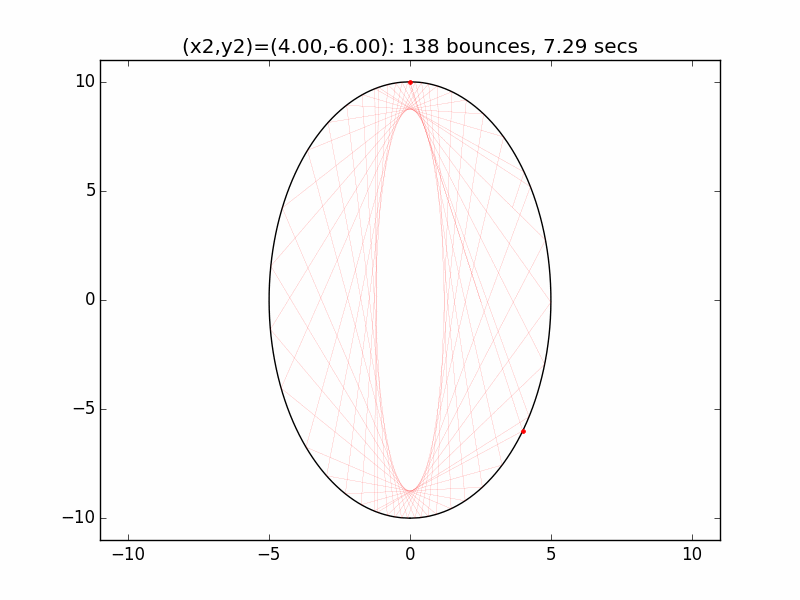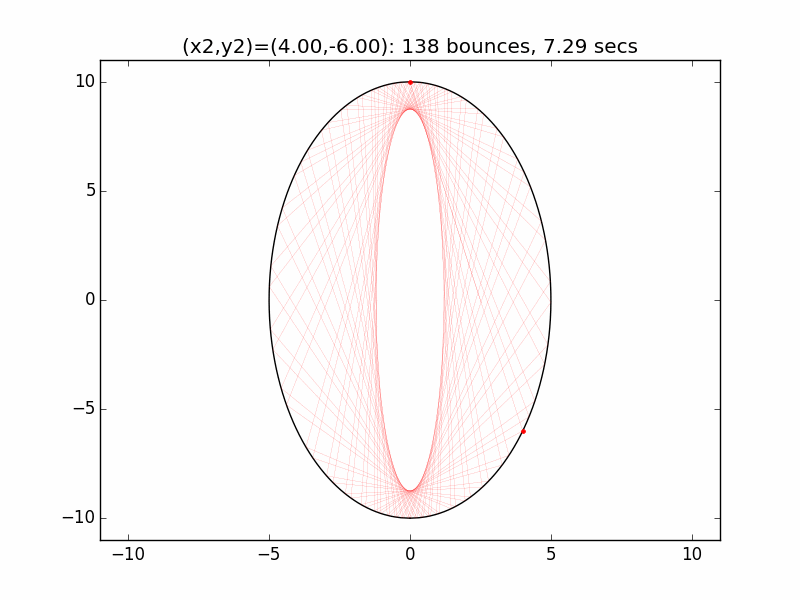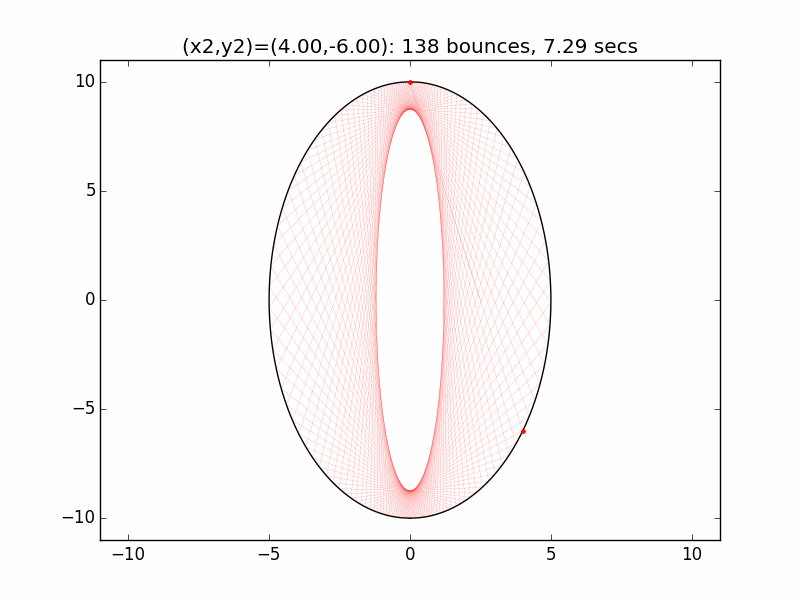
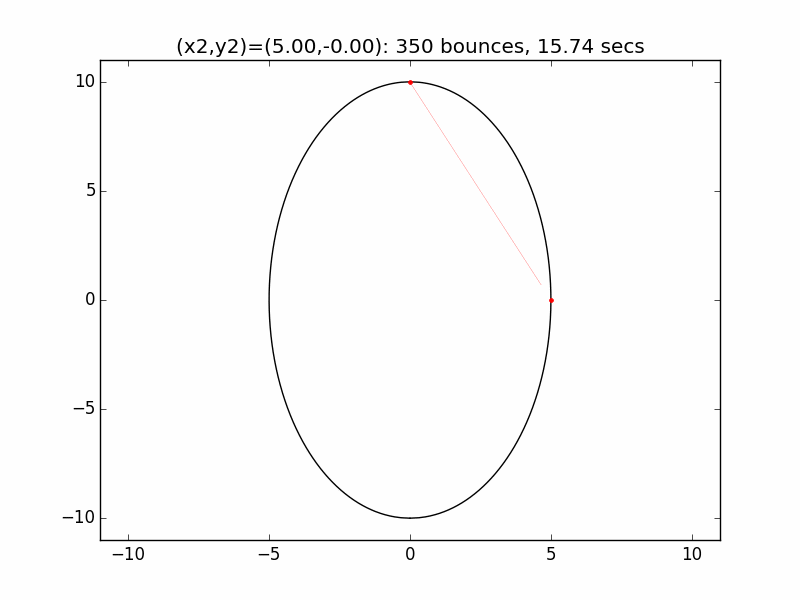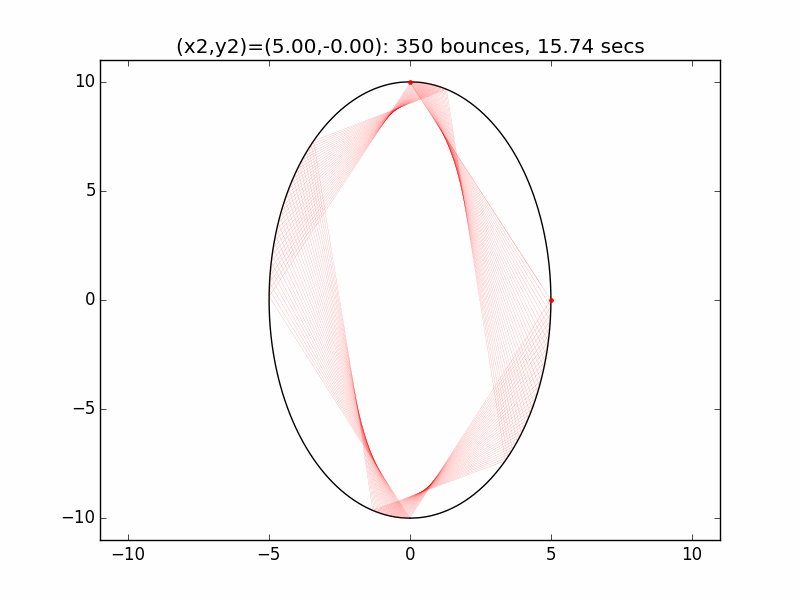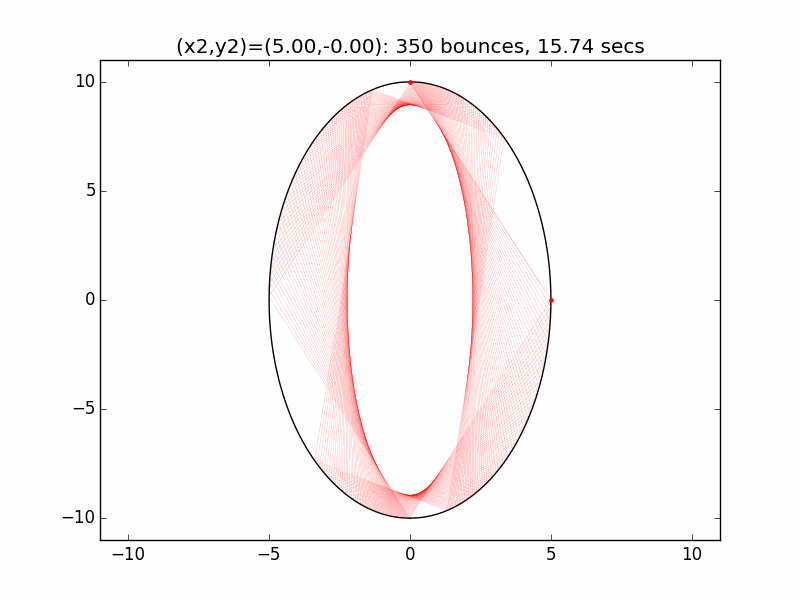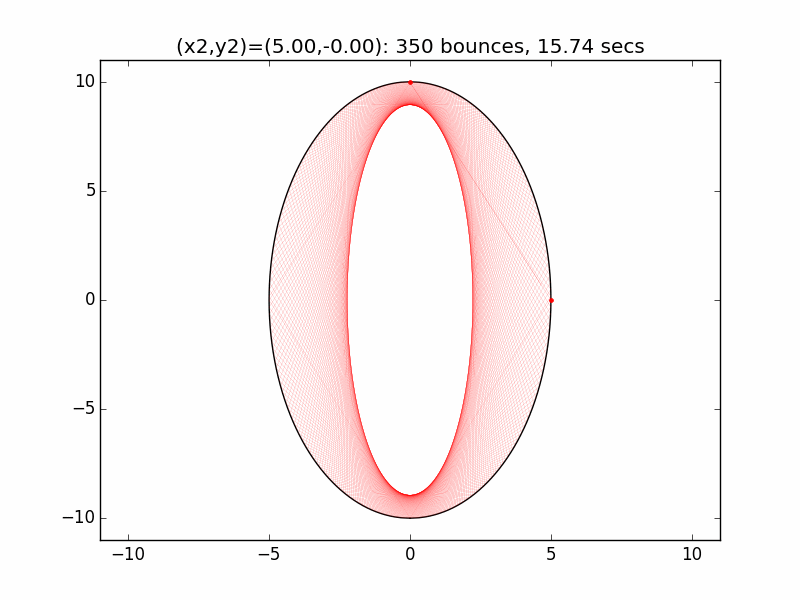
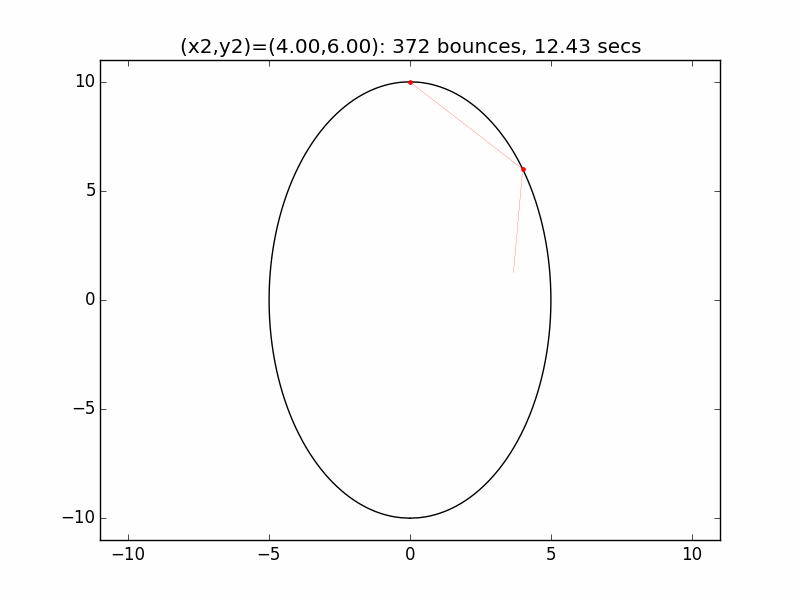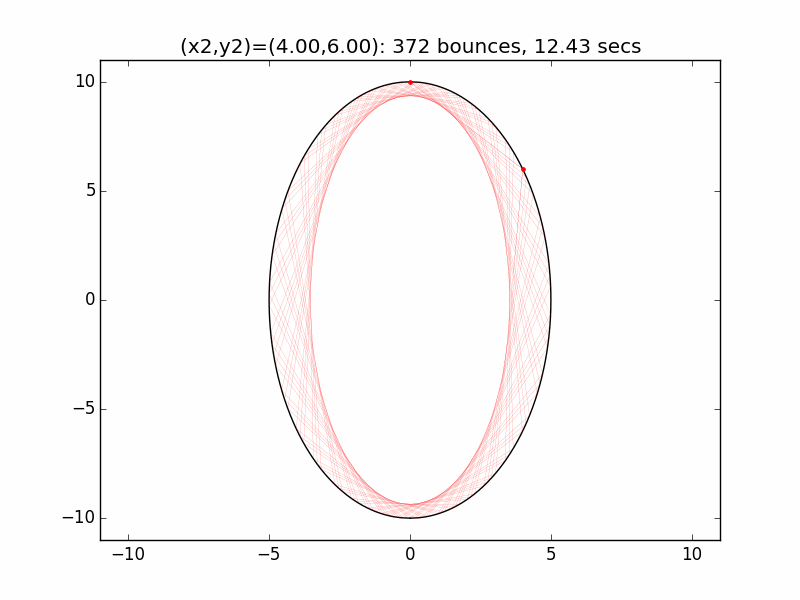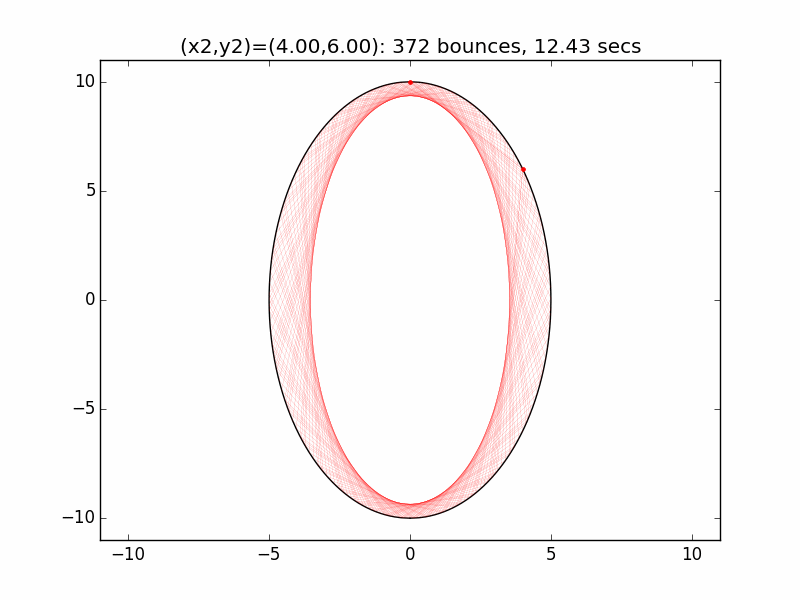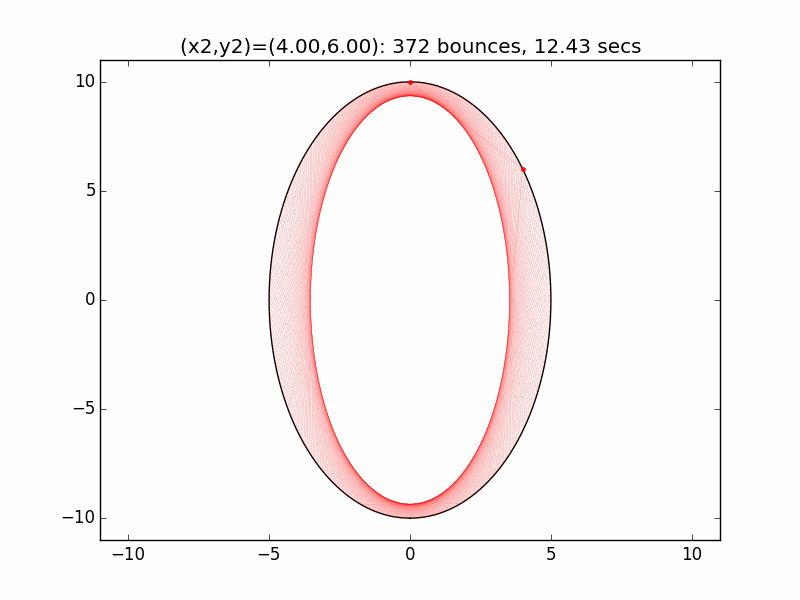
The system is an interesting one to model. The simulations I've graphed here all use a different initial emission point (x1,y1) for the laser beam than in the Project Euler problem: (-0.01,10), just above the left lip of the pinhole. I've set the speed of the beam to be 250 units per second, and modeled the beam path for each of six different initial angles set by choosing the first reflection coordinate (x2,y2). The (-0.01,10) emission point and first reflection point are marked with red dots.

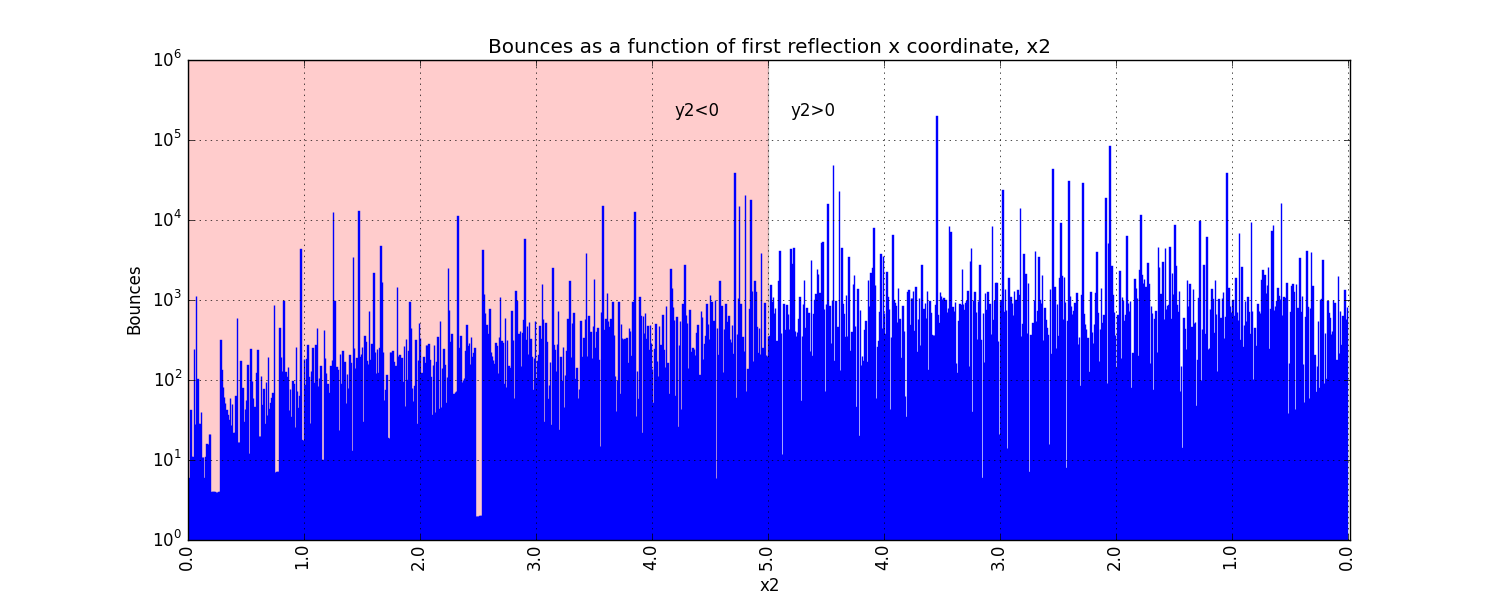
Small changes in initial angle can result in large variations in escape time. Varying the x coordinate of the first relection point in increments of 0.01, the time can go as high as 99 minutes, 5.47 seconds (198636 bounces), for (x2,y2)=(3.56,7.02).

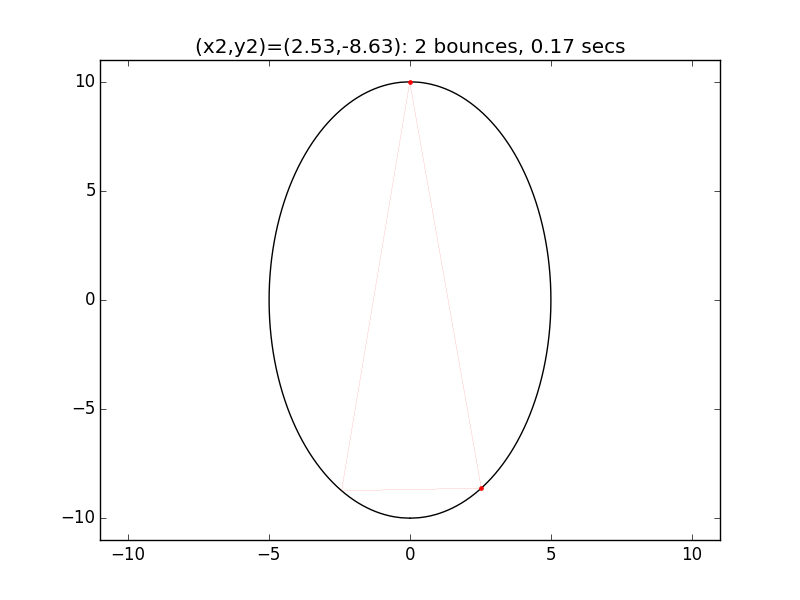
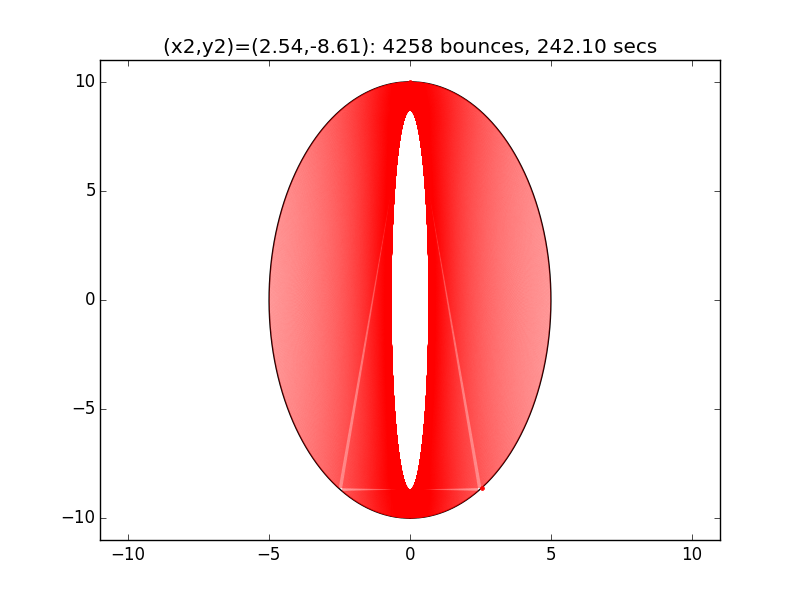
One example of the wide swings in escape time can be seen for x2=2.53 and x2=2.54. In the first case, the beam escapes after only two reflections. In the latter the (not-quite-closed) triangle made by the beam path precesses entirely around the ellipse, with the beam traversing much of cavity multiple times before reaching approximately the same path as in the prior case after 4258 hits and 242.1 seconds.