Contents

% USAGE   : [signal_recovery, res] = sieving(y, struct('threshold', threshold, 'N_band', BW))
% FUNCTION: Perform modulo unfolding using the ITERSIS algorithm
%           from the noisy modulo signal y.
% INPUT   : * y - the noisy modulo signal
%           * MSEbudget - the RMSE of the noise
% OUTPUT  : * signal_recovery - reconstructed signal
%           * res - residue from the algorithm

% DATE    : Dec 2024
% AUTHOR  : Ruiming Guo and Ayush Bhandari
% CONTACT : ruiming.guo@imperial.ac.uk, a.bhandari@imperial.ac.uk
% PAPER   : Ruiming Guo and Ayush Bhandari
%           "ITER-SIS: Robust Unlimited Sampling Via Iterative Signal Sieving"
%           DOI: 10.1109/ICASSP49357.2023.10094780
%           IEEE Intl. Conf. on Acoustics, Speech and Signal Processing (ICASSP), IEEE, Jun. 2023.

% Clear workspace and close figures
clear all;
close all;
clc;

Define Modulo Operator

This function applies modulo operation to input signal x with a threshold.

m_l = @(x, threshold) 2 * threshold * (x / (2 * threshold) + 1/2 - floor(x / (2 * threshold) + 1/2) - 1/2);

Simulation Parameters

Number of samples

N = 100;
n = [0:N-1].' - floor(N/2) + eps;  % Time index with small epsilon to prevent singularities

% Signal Bandwidth (Hz)
Omega = 1000 * 2 * pi;  % Convert to radians per second

% Sampling step
T = 2 * pi / Omega / 20;  % Sampling period

Generate Bandlimited Function

Bandlimited function in the form of a sinc function

x = sinc(Omega*n*T./pi) + 0.6.*sinc((Omega*n*T-5)./pi) - 0.8.*sinc((Omega*n*T+12)./pi);

% Folding Threshold (set to 1/5 of max amplitude)
lambda = max(abs(x)) / 5;

Generate Modulo Samples

Apply modulo operation to generate folded (wrapped) signal

s = m_l(x, lambda);

Additive Noise Model

snr = 15;  % Signal-to-noise ratio in dB
noise = randn(N, 1);  % Generate Gaussian noise
noise = noise / norm(noise, 'fro') * norm(s, 'fro') * 10^(-snr/20.);  % Scale noise to desired SNR
sigma = norm(noise, 'fro') / sqrt(N);  % Compute noise standard deviation

% Generate noisy folded samples
y = s + noise;

Perform Modulo Unfolding with IterSIS Algorithm

Define digital bandwidth for IterSIS

BW = [0, ceil(2 * Omega * T / (2 * pi) * N / 2) + 1];

% Apply the IterSIS algorithm for signal recovery
tic;
[x_itersis, res] = sieving(y, struct('threshold', lambda, 'N_band', BW));
toc;

Elapsed time is 0.334720 seconds.

Compute RMSE of Recovery

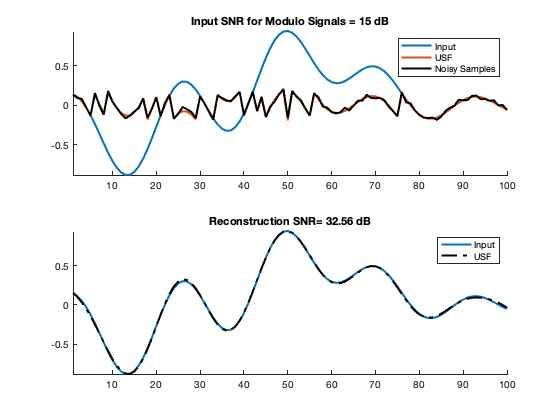
RMSE = norm(x_itersis - mean(x_itersis) + mean(x) - x, 'fro') / sqrt(N);

sig_snr = @(x,xn) 10*log10 (sum(abs(x).^2) / sum(abs(x - xn).^2));

% Display noise and reconstruction performance
disp(sprintf('Noise level is %.2fx10^%d and recovery RMSE is %.2fx10^%d.', ...
    sigma / 10^(floor(log10(sigma))), floor(log10(sigma)), ...
    RMSE / 10^(floor(log10(RMSE))), floor(log10(RMSE))));


subplot(2,1,1)
hold on;
plot(x)
plot(s)
plot(y,'k')
axis tight
title(sprintf('Input SNR for Modulo Signals = %g dB',sig_snr(s,y)))
legend('Input','USF','Noisy Samples')


subplot(2,1,2)
hold on;

hold on;
mat = [x_itersis(:) x_itersis(:).^0];
rec = mat*(mat\x);

plot(x)
plot(rec,'k-.')
axis tight
title(sprintf('Reconstruction SNR= %0.4g dB',sig_snr(x,rec)))
legend('Input','USF','Noisy Samples')

Noise level is 1.84x10^-2 and recovery RMSE is 1.05x10^-2.

Published with MATLAB® R2021a