
Figure 1: A comparison of several machine architectures.
"Processing units" includes all computational elements operating in parallel,
not just ALUs.
ABSTRACT
The computational demands of encoding and decoding motion-compensated transform representations of digital video are well-known, and even hard-wired solutions to single algorithms remain a design challenge. When interactivity or personalization are added, and when algorithms increase in complexity to include structured or object-based representations, not only do the requirements increase but so too does the need for computational flexibility.
It is often proposed to solve the computational problem in a flexible manner by using multiple identical general-purpose processors in parallel (a multiple-instruction, multiple-data, or MIMD approach). Such methods, though, may not achieve the needed number of operations per second without large numbers of processors; in that case communications bottlenecks can arise and programmers can find difficulty in efficiently parallelizing software. A less-well-known form of parallel computation, based on streams, is conceptually closer to to the ways in which people think about algorithms and seems to the authors to offer a more cost-effective, scalable, highly-integratable approach to flexible computing for video.
In this paper, we explain the concept of stream-based processing, and describe why it is a good match to video data. Stream-based computing combined with automatic resource allocation can make the parallelization of the computation automatic at run-time, permitting scalable computing (the same software runs on differently-configured systems) and multitasking. Within this framework, we discuss our implementation of streams on Cheops, a compact data-flow digital video processor developed by the MIT Media Laboratory. We also discuss stream implementations on several other architectures, and how to apply the lessons learned to future programmable hardware for digital video processing.
INTRODUCTION
It is widely known that the computing requirements for digital video are extremely demanding in such applications as compression/decompression, signal processing, and special effects. Even though custom integrated circuits or computational optimizations for general-purpose processors are showing promise of meeting the needs of the current generation of algorithms, algorithms and applications are on the horizon that require tens to thousands of times more operations per second and corresponding memory-to-processor bandwidth.
In order to provide more compression, more flexibility, and more semantic description of scene content, video will in coming years increasingly move toward representations in which the data are segmented not by arbitrary patterns like blocks of pixels, but rather into objects or regions determined by scene-understanding algorithms. The result will effectively be a set of objects and a ``script'' describing how to render them into images. In another paper, we have described the advantages of this approach, and have shown a structure for decoding flexible, object-based video representations.[1] Even aside from advanced video coding methods, computational needs for video are likely to increase greatly in coming years: digital video -- unlike digital audio -- is far from operating at human perceptual limits, and when the display technology and communications bandwidth become available, super-HDTV systems will add to the computational demands. Holographic video displays such as those developed at the MIT Media Laboratory increase the requirements still further.[2]
To understand how we might begin to address the problem, we should examine the characteristics of both digital video data and typical processing algorithms. Relevant points to note about video data are:
Most algorithms of interest, though, do not need simultaneous access to the entire data array. Specifically:
In order to meet the computational requirements of digital video, two techniques: parallelism and specialization, are typically used. The use of multiple processing units operating in parallel is a natural approach to obtaining performance difficult to achieve with a single unit. The specialization of the processing units and their interconnection for implementing a particular algorithm usually allows a significant improvement in performance for a given amount of resources. It is common for varying degrees of both techniques to be used in a particular machine architecture. Figure 1 indicates these parameters for a number of architectures used for video processing.

Figure 1: A comparison of several machine architectures.
"Processing units" includes all computational elements operating in parallel,
not just ALUs.
At one extreme of the tradeoff between generality and performance are specialized processing units using fixed communication networks, as found in application-specific integrated circuits (ASICs). These architectures have traditionally taken advantage of a manual partition of the algorithm along with fixed processor interconnections to achieve the amount of parallelism required. The limitation of specialized processors lies in their inefficiency (or inability) when implementing algorithms outside a particular range. The ability of an architecture to efficiently implement a wide range of algorithms -- its flexibility -- is important for several reasons. Aside from the need for more manipulable video representations, there are already a variety of standards for audio and video representations as well as wide variations within a particular standard.
At the other extreme of specialization are architectures consisting of a network of homogeneous general-purpose processing units, such as the IBM Power Visualization System.[3] General-purpose processors individually don't provide enough processing power, requiring that many be used in parallel. This approach is costly, and the large amount of processing unit parallelism required is problematic. It is difficult to build low latency interconnection networks for a large number of processors, and programming such a multi-processor system is difficult. While the search for a mechanism for audio and video processing which exploits parallelism and takes advantage of specialized processors led the authors to the stream mechanism, streams also alleviate some of the problems associated with general-purpose processor systems.
THE STREAM MECHANISM
The stream mechanism is a mapping of a multidimensional data array into an ordered one-dimensional sequence of data by means of an access pattern. Such a stream mechanism allows for simplified storage, communication, and processing of multidimensional data. When we consider algorithms in a stream-based computing environment, we don't think in terms of a processing element reading or writing memory. Instead, an access pattern turns a source array into a one-dimensional sequence that flows through a processing element and then (through an access pattern again) into a stored (or played, or displayed) destination array. The algorithm can thus easily be described in terms of a graph structure connecting storage buffers with computational elements -- a feature that as we will later see has important advantages in parallelization, hardware scalability, and graphical programming methods. A multiprocessing system which uses streams may be viewed as a multiple-instruction, single-data (MISD) architecture,[4] although the individual processing elements may themselves be SISD, SIMD, or MIMD in nature. A processing pipe architecture is simply a statically scheduled implementation of streams. The stream mechanism is well suited to algorithms where the same operation is applied to a large amount of data, such as those used in image processing.
The concept of a stream has been used extensively in the fields of program semantics and programming languages since the early sixties. The motivations for using streams, along with the actual stream definitions, have varied. A precursor to streams was a similar mechanism, ``coroutines'', which may be described as a set of cooperating processes. Coroutines emphasized modular design, while at the same time minimizing the amount of intermediate storage required by a large application. A good introduction to coroutines, along with a brief history, is that by Knuth.[5]
The search for programming languages that effectively express the parallelism inherent in an algorithm (i.e. non-operational languages) provided further impetus for the development of the stream mechanism.[6][7] The ability of a stream to provide a method for formally representing variables that change dynamically over time was used in several seminal declarative (or applicative) programming languages such as DFPL, VAL and Lucid.[8][9][10][11] The stream definition used was typically an ordered sequence of scalar values. Although streams of compound objects were sometimes supported (in particular, a stream of streams), these stream definitions were exclusively one-dimensional. Specific details of more recent stream implementations will be described later.
The Lucid
language was developed in an attempt to create a
mathematically provable programming language, based on intensional logic.
Although the original version allowed streams only to
represent values changing in time, the current version of Lucid has
been extended to support multidimensional streams.[11]
The value (extension) of variables and expressions in an algorithm
programmed in Lucid depends on an implicit index. Accesses to
Lucid streams are not restricted to the current index, but must be
addressed relative to the current index along a particular dimension.
Intensional programming
formalizes and simplifies the specification of
functions that operate over 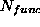 dimensions but are applied to
datasets of dimensionality
dimensions but are applied to
datasets of dimensionality 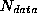 such that
such that 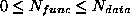 .
.
The stream mechanism we are proposing differs from the previous examples in that it defines the intensional mapping between the multidimensional array and the one-dimensional stream sequence (the access pattern) to be used at the source and destination of each stream. The properties of those mappings are then used to determine implementation requirements such as buffering requirements and available data parallelism.
The previous examples of stream mechanisms are typically utilized in a system implementation in two distinct manners: In many cases, ([9][11][12]) a stream mechanism is utilized only for purposes of algorithm specification. Once the algorithm is translated for execution, the data is treated as an ordered sequence of individual data objects. In this data-flow model, ``tokens'' consisting of single instructions along with a reference to data values to which they should be applied are generated for each array element in the stream. Another approach, supporting a stream primitive data object, allows efficiencies in data storage not possible in the pure data-flow model.[13][14][15] The former approach provides the maximum parallelism, but incurs a high scheduling overhead and is usually proposed for execution only on fine-grained data flow architectures. The latter approach is amenable to a coarser granularity of processing, which allows the amortization of the scheduling overhead over a number of stream data elements.
The set of possible mappings, or access patterns, from a multi-dimensional data space into a single sequence is not finite, and in many interesting cases it is difficult to determine a priori . We propose supporting a particular set of access patterns typical to image processing routines, capable of performing a single level of regular scattering or gathering in an arbitrary number of dimensions.
Collapsing a multidimensional array down to a sequence of values
conceptually involves a set of nested, bounded, integrally-incremented
array index counters. We can describe the behavior of these virtual
counters by a set of four integer parameters per
dimension. Establishing the starting location, or origin ( e.g.
suppose we want the values in odd-numbered locations) requires an
initial offset value. We will refer to the maximum range of
array indices in a given dimension as the extent. The
step parameters give the counter increment and initial location in
each dimension. There are several ``special'' values that a step
parameter may have for a particular dimension. One is zero, which
indicates that the same values are to be replicated along that
dimension. The value of the extent along any dimension of the stream
(denoted by 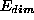 ) may also be
specified as a step parameter,
allowing the multidimensional array to be stored in a ``packed''
format. The order of counter nesting ( i.e., do we scan
horizontally and then vertically, or vice versa) is specified by what
we will call the order parameters.
) may also be
specified as a step parameter,
allowing the multidimensional array to be stored in a ``packed''
format. The order of counter nesting ( i.e., do we scan
horizontally and then vertically, or vice versa) is specified by what
we will call the order parameters.
Although the dimensions are interchangeable, it is convenient for a system to attach a meaning to each. We will call the lowest dimension the Sample dimension, and typically use it for the characteristics of a particular sample (such as the color components of a pixel). We assign the next three dimensions, in order of increasing dimensionality, to the Horizontal, Vertical, and Temporal dimensions.
It is often the case, though, that we need to scan through multidimensional subarrays of our larger array (consider dividing images into 8-by-8 tiles), and in order to do that we need to specify another layer of iteration, using the same parameters we've already defined. We will call the description of the upper level of counters the block parameters and the lower-level ones the sample parameters. The sample access pattern parameters determine the nature of the scatter or gather operation, whereas the block parameters determine how the data from the individual samples is sequenced. The data array does not need to be continuous over the entire range in every dimension, i.e. it may be sparse. The extent of any dimension may be constant, bounded by a constant, or infinite.
We will use the following data array (having an extent of {1, H, V, 1}
-- thus it might be a monochrome single video frame) as the
source for example streams illustrating the different parameters:

The first example is a common raster scan, with a horizontal decimation
by two. It has the following access pattern parameters:
block extent{ 1, H/2, V, 1 } block step{ 0, 2, 1, 0 }
block order{ 0, 1, 2, 0 } block offset{ 0, 0, 0, 0 }
sample extent{ 1, 1, 1, 1 } sample step{ 0, 0, 0, 0 }
sample order{ 0, 0, 0, 0 } and the resulting stream sequence
(assuming H even) is:

Another common access pattern is a raster scan of sequential tiles of data,
in this case 8-by-8 blocks of data.
It has the following access pattern parameters:
block extent{ 1, H/8, V/8, 1 } block step{ 0, 8, 8, 0 }
block order{ 0, 1, 2, 0 } block offset{ 0, 0, 0, 0 }
sample extent{ 1, 8, 8, 1 } sample step{ 0, 1, 1, 0 }
sample order{ 0, 1, 2, 0 } and the resulting stream sequence is:

One use of the access pattern is to describe how a multidimensional data array is stored in a memory device that only supports a linear address space ( i.e. most memory devices). The other use of the access pattern is to describe how an algorithm segment (hereafter referred to as a function) would traverse the multidimensional data if accessing it directly, both for input and output. Note, however, that a function's access pattern specifies only the data traversed in a single application of the function. A stream usually consists of this access pattern repeated as many times as possible over the extent of the stream source. For example, a block transform function only specifies how it wants the input data sequenced within the block, but not how the blocks are sequenced within an image (or sequence of images) to produce the input stream.
Some useful access patterns ( e.g. the zig-zag scan used on block transform coefficients, or serpentine scans used to hide processing artifacts) are not describable using the above simple, monotonic access pattern. In these cases it will be necessary for a processing element to perform the reordering itself. Here we rely on the observation that in general these non-monotonic patterns operate over a relatively limited area in each dimension -- a block already defined using the mechanism provided -- and thus the processing element need not maintain a large amount of state in order to map into and out of them. The tradeoff here is between the complexity of the address generation hardware and the amount of local storage required in a processing unit.
There are a number of common operations (such as convolution, or motion estimation) that operate over a ``neighborhood'' or window of input data which is moved only incrementally between function evaluations. Using the above access pattern definition, this neighborhood is indicated independently for each dimension, and is defined as the sample extent times the absolute value of the sample step -- if the step is non-zero -- and one otherwise. The size of the ``sample overlap'' along each dimension is equal to the sample neighborhood minus the absolute magnitude of the block step.
If the sample overlap is non-zero, the runtime scheduler will attempt to pipeline the stream operation, thereby amortizing the cost of transferring the overlap over as many blocks as feasible. Pipelining is possible when the function can be executed on a processor that has sufficient local storage to store stream values that it will need again. In the one-dimensional case, there must be sample_extent stream values of memory. In the N-dimensional case, there must be enough memory to store the multiple of the block extent times the sample extent for each of the N-1 lower dimensions (as indicated by the block order). When it is desirable to pipeline the processing of data extents larger than the local storage provided by the processing units in a system, the stream may be automatically partitioned into multiple smaller streams in order to avoid overflowing the processor local memory, in a manner identical to that used for exploiting data parallelism (see the following section).
In implementation, a stream system may consist of specialized processors using hardware to implement the stream communications, or general-purpose processors in a shared memory configuration using memory buffers to perform all communications. Or, ideally, it may combine general-purpose and specialized processors into a heterogeneous system using both stream implementations. In either case, the access parameters of the stream source and destination along with the relative rates of processing and the processing granularities are sufficient for estimating the amount of temporary buffering that a stream will require. Temporary buffers may be inserted into streams between two algorithm segments if necessary. If access patterns of both the stream source and destination are identical, the stream requires only enough buffering to overcome differences in processing rates, algorithm-specific delays, and variations in data throughput (which might be a very small amount). If the access patterns are different and non-changeable, the amount of buffering required is a multiple of the union of the two access patterns.
If multiple functions utilize the same stream, the stream must be conceptually split. This requires that enough stream buffering be provided to account for differences in the data consumption along multiple stream paths. Some stream languages require that this delay be explicitly defined by using a delay element.[18] We believe that an appropriate buffer size may be estimated using information about function latency, in addition to the delay value explicit in the offset parameter. The average rate of data consumption on all paths of a split must be equal, otherwise the amount of storage required is unbounded. Overflow of a stream's buffering resources results in the stream source being stalled. In some implementations, the size of the stream buffering may be increased at runtime by the resource manager. Also, the stream buffers may be paged out to slower storage to allow for longer delays.[13]
Many common functions produce and consume data at different rates. Explicit information about this is provided by the block extent parameter of the function's stream input/output access pattern, and is used by the resource manager to help determine the amount of buffering required along a stream. For an interesting class of functions, such as entropy coders, the input or output rate is not constant (it is instead data dependent), but to allow implementation it must be bounded.[9][15]
All the access patterns discussed to this point have been determined by the algorithm. Another important class of access patterns are those which are data dependent, such as those produced by motion estimation, image warping, or use of a lookup table. Although these streams do not exhibit the same degree of locality and periodicity as the data independent access patterns, some access locality will generally be present for use by a caching system.

Figure 2: A simple task -- video mixing -- shows the
differences between control and data parallelism.
STREAM PARALLELISM
Exploitation of multiple processing units in a scalable design requires that segments of algorithms be executable in parallel. There are two methods for achieving parallelism (Figure 2). Different algorithm segments may be executed at the same time by different processing units, providing control parallelism. The other method, data parallelism, is when an algorithm segment that is being applied to a large data structure is executed in parallel upon subdivisions of the data structure by different processing units. The stream mechanism explicitly supports both methods of parallelism.
Streams provide a synchronization mechanism between algorithm segments operating in parallel, in support of control parallelism. The producer and consumer of a stream of data may execute in parallel, and doing so may greatly reduce the amount of temporary storage required by an algorithm. Streams also impose a programming style which strongly encourages a modular approach to algorithm specification, making medium and coarse grained control parallelism more evident. In addition, many of the programming languages utilizing the stream mechanism (Lisp, SISAL, Lucid) were designed with the identification of control parallelism as a goal.
It is in identifying and utilizing the data parallelism inherent in an algorithm, however, that streams are adept. Depending on scheduling granularity decisions at runtime (described later), a stream may be subdivided (or ``scattered'') for concurrent processing, with the resulting streams being consolidated (or ``gathered'').[16] This partitioning of streams is supported by the above parameterized access pattern. In the case of streams where one of the dimensions of the (possibly virtual) source data array is unbounded (usually time), partitioning is also performed to discretize the continuous processing into segments for scheduling purposes.
The number of processing operations scheduled for execution as a single unit (the granularity of the scheduling) depends on both the machine architecture and the algorithm being executed. A finer granularity of scheduling provides more opportunities for parallelism, but incurs a high scheduling overhead. The scheduling granularity of an algorithm on a stream based system, while generally coarse (commonly 2000 or more processing operations) may be varied at runtime to match more closely the machine architecture. The granularity may be varied on a function by function basis by partitioning (or varying the partition size) of the streams to allow data parallelism. The lower bound to the stream partitioning is determined by the extent of the access pattern of the function, and the scheduling overhead associated with a finer granularity. The upper bound is determined by the buffering resources required between the processing blocks, the extent of the stream source(s), and the number of processing units on which execution will take place. Determining the optimum granularity for execution of a particular algorithm on a particular machine is one of the tasks of the runtime resource manager.
THE ROLE OF A RESOURCE MANAGER
A runtime system for managing resources provides a number of critical services. It allows an algorithm to be executed on a variety of platforms by mapping the algorithm onto the available number and type of processing units. At the same time, it allows applications executing concurrently to share a limited pool of resources, providing for graceful degradation of a system (fair access to resources) when overloaded. Finally, it performs the run-time partitioning of streams to exploit data parallelism. We propose that all stream systems, with the exception of the simplest ones (which may be statically scheduled), will require a resource manager responsible for managing computational, storage, and communications resources.
The resource manager is responsible for deciding which processing unit should be used to execute a particular algorithm segment. This decision is based on how efficiently a particular processing unit will perform the task, the amount of local storage required for efficient pipelining, and the complement and current usage of processing units in the system. Mapping the algorithm segment onto a processing unit may be as simple as selecting one code segment from a set pre-compiled for general-purpose or specialized processors, or involve interpreting (and caching for possible re-use) a generic byte-code into an executable code segment. The task of programming an algorithm for real-time execution is facilitated by the resource manager, which accepts the responsiblity for scheduling tasks in an optimum manner for meeting a constant input or output rate constraint.
Memory resources are allocated and automatically deallocated by the resource manager. This allows an algorithm to operate independently of a particular memory architecture -- the resource manager may allocate storage in a location it deems optimal for that algorithm and architecture. In addition, automatic deallocation (``garbage collection'') of memory objects greatly simplifies the application programmer's task.
The manner in which communication resources are managed varies with machine architecture. Some architectures use communication resources such as shared buses, or packet-switched networks, which rely mainly on fast hardware arbitration. Others use semi-static routing -- such as a circuit-switched crossbar -- or DMA channels, which must be scheduled. The resource manager both takes the availability of the communication resources into consideration when scheduling algorithm segments, and performs any initialization of communications channels ( e.g. configuring the crossbar, or DMA controller) required.
While the above functions of a resource manager are identical to those of a modern operating system,[17] there are additional functions imposed by the stream mechanism. The manager must determine the granularity of scheduling appropriate for the algorithm and architecture being used (as described in the previous section). It then partitions the streams to match the granularity selected, and pipelines the stream access to eliminate as much sample overlap as possible. The pipelining must be done at run-time, after processing unit storage capabilities and other concurrently-executing tasks are known. The resource manager is responsible for actually creating the streams in an algorithm, which entails allocating the temporary buffers required (if any). It also implements a coarse grain stream synchronization mechanism -- when data are available in a stream the destination is notified/applied. Deallocation of the stream buffers is handled automatically as for any memory object.
IMPLEMENTATIONS
In the following paragraphs we discuss the implementation of streams on four different machine architectures: two similar machines using specialized processing units and explicit support for streams, a shared memory MIMD machine, and a single general-purpose processor machine.

Figure 3: The Cheops processor connects
specialized processors to DMA-equipped banks of memory through a
crosspoint switch. Resource allocation and user interaction are
handled by an Intel 80960CF processor. The Nile Buses are high-speed
DMA channels used for transferring data from module to module.
Cheops
The Cheops processor module (Figure 3) -- developed at the MIT Media Laboratory -- is a board level system containing up to eight heterogeneous specialized processing units (stream processors) connected through a full crosspoint switch to a set of eight memory units. Each memory unit is independently capable of sourcing or storing one stream, although the access pattern supported is simpler than the one described above -- only one level of access pattern is supported, and only for two dimensions. A general-purpose processor is used to execute both the resource manager and algorithm segments which don't map well onto the specialized stream processors provided. The crosspoint switch is semi-statically switched by the resource manager to configure a processing pipeline for a particular stream segment, while a separate hardware handshake mechanism is used to synchronize the actual stream flow.[2][19]
The stream processors are optimized for performing a set of common image processing operations. One of them, for example, consists of eight 16-bit multiply-accumulate units, a tree of adders for combining the results, and 64 words of local storage. It is used for 1-D convolution, matrix multiplication, and simpler stream functions using multiply and or addition (such as scaling and mixing). Other processors are specialized for motion estimation, motion compensation, image warping, hidden surface removal, block transform coding, and basis vector superposition.
The limitations of the Cheops architecture are mainly due to departure from the stream mechanism described above. The inability of the address generators to support two levels of iteration, though mitigated by stream processors with sufficient local storage to allow stream pipelining, prevents efficient processing of arrays of vectors. The constraint of one stream per memory bank, along with the small number of memory banks, strongly limit the parallelism that may be achieved. In spite of these limitations, the performance of a Cheops system on image processing algorithms (examples in [19]) is still significant.
A Video Signal Processor
Philips' Video Signal Processor (VSP) is a commercially available monolithic processing unit designed for operating upon video streams. A single chip contains twelve arithmetic/logic units, four memory elements, six on-chip stream buffers, and ports for six off-chip streams, all interconnected through a full crosspoint switch. The processing units are programmable, but limited to a single operation per cycle, and have no internal state or local storage. This means that even an operation as simple as multiplication requires multiple passes though a processing element. The stream buffer elements provide a fixed length delay of up to 32 words. The memory elements consist of 2K words of memory, which may be used as either a longer buffer element or a lookup table. Either or both the read and write addresses for accessing the memory elements may be generated from a stream.[20]
The VSP implements a rather restricted version of streams, in several respects:
A Shared Memory Multiprocessor
Texas Instruments' TMS320C80 Multimedia Video Processor (MVP) is a monolithic MIMD multi-processor, with a non-uniform access shared memory architecture. Four digital signal processing units (ADSPs), along with one general-purpose processor (MP), are interconnected through a crosspoint switch to nineteen 2 KByte memory banks. Each processor may also access off-chip memory directly, even though a versatile transfer controller (TC) is also provided for DMA transfers.[21]
The stream mechanism is easily implemented on the MVP, due to the large amount of storage local to the processing elements and the flexibility of the interconnection network. Stream temporary buffers are located in the on-chip memory, where software running on the ADSPs and the MP may efficiently access it. The resource manager is executed on the MP, and it is responsible for using the TC to transfer stream data in and out of the temporary buffers, as well as scheduling algorithm segments for execution on the ADSPs and the MP.
The communications latency between an ADSP and an on-chip memory bank is bounded by a small number, due to the arbitration strategy of the crossbar. In particular, if no other processing units are accessing that particular bank the latency is fixed and small, allowing proper sequential instruction generation to make it negligible. The communications latency between an ADSP or on-chip memory and an off-chip device is variable and bounded by a much larger number, in many systems, making a (decoupled) stream approach to off-chip communications attractive.
Single Processors
Even machines with a single general-purpose processor may utilize the stream mechanism to their advantage. While such a machine is incapable of exploiting either control or data parallelism of the granularity provided by streams, performance improvements may still be obtained as a result of the clearer definition of the data access patterns. The goals of a stream mechanism within the von Neumann machine model are similar to those of compiler vectorization techniques. Pipelining of the stream sample overlap, for example, is an explicit form of the technique of recurrence detection infrequently used by optimizing compilers to minimize memory access.[5][22]
While unable to exploit the additional data parallelism provided by partitioning a stream, a single processor machine may nonetheless benefit from partitioning of large data sets such as images. In a similar technique for array processing, ``tiling'', permutation of loop constructs is performed to increase the locality of an algorithm's memory access. This is usually done to increase the performance of a data cache, although it may also be applied simultaneously to optimize the use of registers.[23] A speed-up factor of 2.75 has been reported for a matrix multiplication algorithm, using an R3000 with a two level cache, due to the improved utilization of local storage.[17]
There have been several processor architectures proposed which included hardware support for a stream mechanism, in an attempt to overcome memory latency.[24][25][26][27] These decoupled, or structured memory access architectures identify the address generation and data access operations (data ``production''), and decouple them from the data processing operations (data ``consumption''). Hardware support is provided for sequential buffering of data retrieved from memory, but not yet consumed. Address generation and data access is performed by a separate processing unit. Although the primary goal of Benitez, et al.,[22] was the automatic detection by a compiler of opportunities for using such a simple streaming mechanism, they report a performance improvement even on traditional platforms (such as 68030, VAX, and 88K architectures.)
CONCLUSIONS
We have presented a definition of the stream mechanism that supports high performance, scalable, parallel processing of large multidimensional data sets, such as audio and video. Streams are a useful method for processing large amounts of data (as in video) regardless of the machine architecture. By clearly identifying a convenient communication mechanism, however, streams simplify the use of parallel heterogeneous processing units. We have attempted to present streams independently of a particular programming model, even though the concept is often associated with the data-flow paradigm.
In conclusion, we note several architectural features that allow optimal implementation of the stream mechanism:
Research described in this paper has been supported by the Television of Tomorrow Consortium at the MIT Media Laboratory.
[1] V. M. Bove, Jr., ``Object-Oriented Television,'' 136th
SMPTE Technical Conference, 1994, paper 136-3.
[2] J. A. Watlington, M. Lucente, C. J. Sparrell, V. M. Bove, Jr., and
I. Tamitani, ``A Hardware Architecture for Rapid Generation of
Electro-Holographic Fringe Patterns,'' Proc. SPIE Practical
Holography IX, 2406, 1995, pp. 172-183.
[3] D. A. Epstein, et al., ``The IBM POWER Visualization System:
A Digital Post-Production Suite in a Box,'' 136th
SMPTE Technical Conference, 1994, paper 136-98.
[4] M. J. Flynn, ``Some Computer Organizations and Their Effectiveness,''
IEEE Trans. on Computers, 21, No. 9, 1972, pp. 948-960.
[5] D. E. Knuth, The Art of Computer Programming: Fundamental
Algorithms, Vol. 1, Addison-Wesley, Reading MA, 1973.
[6] G. Kahn, ``The semantics of A Simple Language for Parallel
Programming,'' Information Processing 74: Proceedings of the IFIP
Congress, Aug. 1974, pp. 471-475.
[7] W. H. Burge, ``Stream Processing Functions,'' IBM Journal of
Research and Development, 19, Jan. 1975, pp. 12-25.
[8] P. R. Kosinski, ``Denotational Semantics of Determinate and
Non-Determinate Data Flow Programs,'' Technical Report TR-220, MIT
Laboratory for Computer Science, Cambridge MA, May 1979.
[9] J. B. Dennis, and K. S. Weng, ``An abstract implementation for
concurrent computation with streams,'' Proc. 1979 Conf. on Parallel
Processing, Aug. 1979, pp. 35-45.
[10] S. J. Allan, and R. R. Olderhoeft, ``A Stream Definition for Von
Neumann Multiprocessors'', Proc. 1983 Int'l Conf. on Parallel
Processing, Aug. 1983, pp. 303-306.
[11] E. A. Ashcroft, A. A. Faustini, R. Jagannathan, and W. W. Wadge,
Multidimensional Programming, Oxford Univ. Press, New York, 1995.
[12] J. L. Gaudiot, ``Methods for Handling Structures in Dataflow
Systems,'' Proc. 12th Annual Int'l Symp. on Computer
Architecture, 1985, pp. 352-358.
[13] L. J. Caluwaerts, J. Debacker and J. A. Peperstraete, ``Implementing
Streams on a Data Flow Computer System with Paged Memory,'' Proc. 10th
Annual Int'l Symp. on Computer Architecture, 1983, pp. 76-83.
[14] R. W. Hartenstein, A. G. Hirschbiel and M. Riedmüller, ``A Novel
ASIC Design Approach Based on a New Machine Paradigm,'' IEEE Journal
of Solid State Circuits, 26, No. 7, July 1991, pp. 975-989.
[15] S. S. Bhattacharyya and E. A. Lee, ``Memory Management for Dataflow
Programming of Multirate Signal Processing Algorithms,'' IEEE Trans.
on Signal Processing, 42, No. 5, May 1994, pp. 1190-1201.
[16] J. S. Onanian, ``A Signal Processing Language for Coarse Grain
Dataflow Multiprocessors,'' MS Thesis, Massachusetts Institute of Technology,
Cambridge MA, June 1989.
[17] K. Hwang, Advanced Computer Architecture: Parallelism,
Scalability, Programmability, McGraw-Hill, New York, 1993.
[18] E. A. Lee, ``Representing and Exploiting Data Parallelism using
Multidimensional Dataflow Diagrams,'' Proc. IEEE 1993 Intl. Conf. on
Acoustics, Speech and Signal Processing, April 1993, pp. I-453 -- I-456.
[19] V. M. Bove, Jr. and J. A. Watlington, ``Cheops: A Reconfigurable
Data-Flow System for Video Processing,'' IEEE Transactions on
Circuits and Systems for Video Processing, 5, no. 2, Apr. 1995, pp.
140-149.
[20] H. Veendrick, O. Popp, G. Postuma, and M. Lecoutere, ``A 1.5 GIPS
Video Signal Processor (VSP),'' Proc. 1994 IEEE Custom Integrated
Circuit Conf., 1994, pp. 95-98.
[21] Texas Instruments, Inc., ``TMS320C80 Technical Brief: Multimedia
Video Processor (MVP),'' Houston TX, 1994.
[22] M. E. Benitez and J. W. Davidson, ``Code Execution for Streaming:
an Access/Execute Mechanism,'' Proc. Fourth Int'l Conf. on
Architectural Support for Programming Languages and Operating
Systems, April 1991, pp. 132-141.
[23] M. E. Wolf and M. S. Lam, ``A Loop Transformation Theory and an
Algorithm to Maximize Parallelism,'' IEEE Trans. on Parallel and
Distributed Systems, 2, No. 4, Oct. 1991, pp. 452-471.
[24] G. S. Sohi and E. S. Davidson, ``Performance of the Structured
Memory Access (SMA) Architecture,'' Proc. 1984 Int'l Conference on
Parallel Processing, Aug. 1984, pp. 506-513.
[25] J. R. Goodman, J. Hsieh, K. Liou, A. R. Pleszkun,
P. B. Schechter, and H. C. Young, ``PIPE: A VLSI Decoupled
Architecture,'' Proc. 12th Annual Int'l Symp. on Computer
Architecture, 1985, pp. 20-27.
[26] J. E. Smith, G. E. Dermer, B. D. Vanderwarn, S. D. Klinger,
C. M. Rozewski, D. L. Fowler, K. R. Scidmore and J. P. Laudon, ``The
ZS-1 Central Processor,'' Proc. Second Int'l Conf. on
Architectural Support for Programming Languages and Operating
Systems, Oct. 1987, pp. 199-204.
[27] W. A. Wulf, ``Evaluation of the WM Architecture,'' Proc 19th
Annual Int'l Symp. on Computer Architecture, 1992, pp. 382-390.
About the preparation of this document
wad@media.mit.edu
Fri Oct 28 1995