

Batch optimization methods could be applied to this model, sequentially processing groups of two or more temporal samples (frames) to resolve the feature "structure" and the camera motion over time. In the limit where only two frames are processed, and there is no camera rotation, this batch optimization approaches stereo vision techniques.
Continuous optimization methods, on the other hand, seem natural due to the continuous nature of the problem. A less obvious advantage is that while the batch method produces an answer that is optimal in the least squares sense across the entire batch, it may not be optimal at any individual frame in the batch. Small noise in the estimated camera motion model, which if zero mean will be ignored by the batch method, may not be noise at all - imagine the slow oscillation of a camera perched on top of a tripod. A continuous method should track the pertubations from the motion model (modeled as "noise"), while diminishing the influence of noise relative to algorithms that estimate based solely on two frames.
Extended Kalman (or Kalman-Schmidt) Filtering (EKF) is a continuous optimum estimation method for models where either the measurement process or the system process is non-linear. Even briefly introducing the Kalman Filter of which is an extension is beyond the scope of this document (see Jazwinski70, Grewal93, Brown92, and Gelb74.)
The block diagram shown below describes an Extended Kalman Filter. All variables are either matrices or vectors. The upper portion (above the dashed line) is the estimation loop. This is where a new estimate of the system state is made, using the input measurements and the a-posteriori (improved by using the input data) estimate of the previous state.
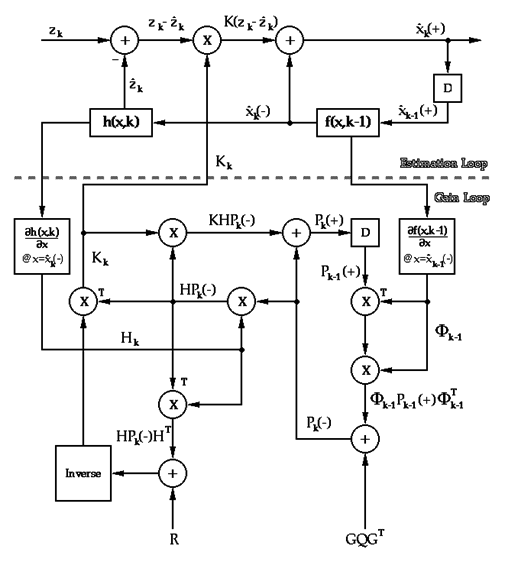
The Iterated Extended Kalman Filter (IEKF) goes even farther...
Despite the earlier critique of batch methods, they can be indispensable. In order to start a Kalman filter, it is necessary to have a good initial estimate of the system state (and the covariance of said estimate.) One the major problems I had in implementing and test the EKF code is its sensitivity to initial estimate covariances.
Levenberg-Marquardt.
The model specific code for both an IEKF and an LM are similar (compare kalman_camera.c and eval_camera.c), both requiring the evaluation of the imaging transformation and its Jacobian at every point for every step or iteration.