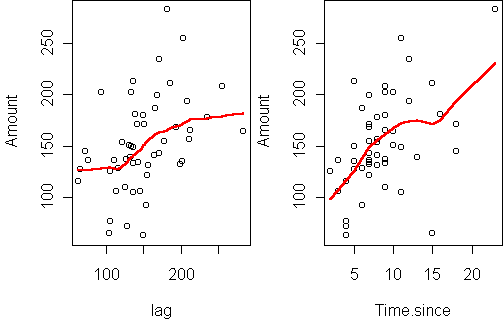
This shows a strong connection with time and a lesser positive correlation with the previous amount. A linear autoregressive model, which predicts Amount based on the previous purchase amount and the time since, can explain 36% of the variance.
A first step toward this goal is to develop a model of an individual's purchasing behavior. As described by Boatwright et al, delivery retailers need models not just of total sales but of the relationship between purchase quantity and purchase frequency. This is because a delivery retailer can increase profits not just by increasing total sales but also by reducing purchase frequency.
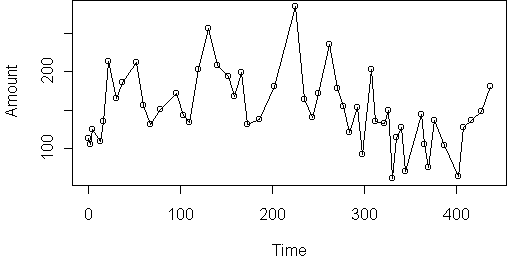
The dataset used here is the same one used by Boatwright et al. It describes the purchase dates and amounts for 14,000 different customers of an online grocer during the years 1996-1998. Here is the data for one of the customers (aa16755):
Time Amount 0 112.98 3 105.37 5 125.07 14 109.84 17 135.89 ...
A better approach is to plot the amount versus the lagged amount and
versus the
time since the last purchase:

This shows a strong connection with time and a lesser positive correlation
with the previous amount.
A linear
autoregressive model, which predicts Amount based on the
previous purchase amount and the time since,
can explain 36% of the variance.
However, an autoregressive model is not an intuitively appealing model of purchasing. So we turn to a different model, in hopes of better performance.
Supply = Initial.supply + Total.purchases - ConsumptionThe first assumption is that the customer has a constant consumption rate:
Consumption = Rate * TimeThe second assumption is that the customer makes purchases in order to minimize the variance of their supply. In other words, the customer minimizes the sum of squares of the supply over time. The third assumption is that the customer is loyal, i.e. they always purchase these particular products at this particular store. Hence the store knows the customer's total purchases. Because we know the total purchases and we know the time, we can rewrite the supply equation into a linear regression problem:
Total.purchases = Rate * Time - Initial.supply + Supplywhere Rate is the slope, -Initial.supply is the intercept, and Supply is the "noise" (the residual of the fit).
To check that these assumptions are valid, it is sufficient to plot the
customer's total purchases over time, and see if it is linear:
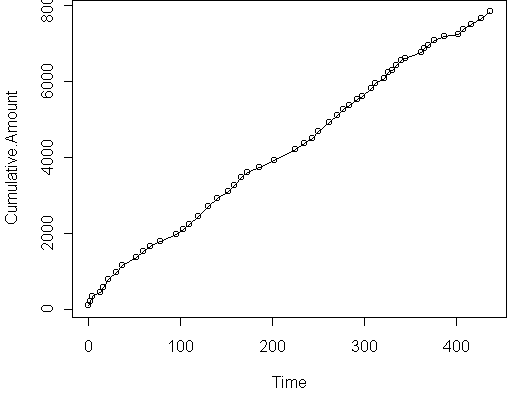
This curve is not perfectly linear, but it does follow locally linear
trends.
An interesting by-product of the resupply model is that we can estimate exactly when the customer shopped elsewhere and how much they spent. To do this, we add extra terms to the regression model representing a sudden change in supply at a particular time. Stepwise regression can automatically tell us which terms are useful. Doing this for the above customer produces the model
(Intercept) Time Time.402 Time.362
251.72 20.57 -382.36 -213.14
Time.96 Time.225 Time.202
-246.77 -237.19 -229.81
The coefficient for Time is the consumption rate.
The Time.X terms are step functions which begin at a particular
time.
This implies disloyalties at times 96, 202, 225, 362, and 402,
with values $247, $230, $237, $213, and $382.
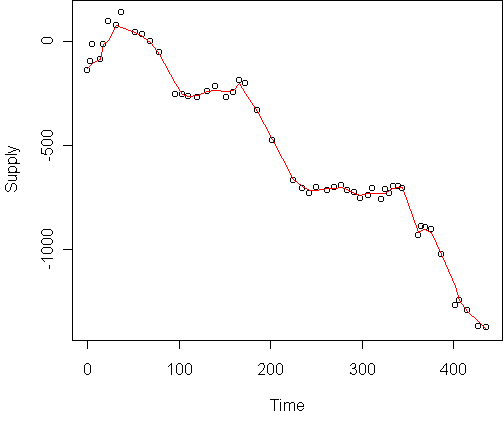
The learned model leads to the following
estimate of supply over all time (disloyal periods omitted):
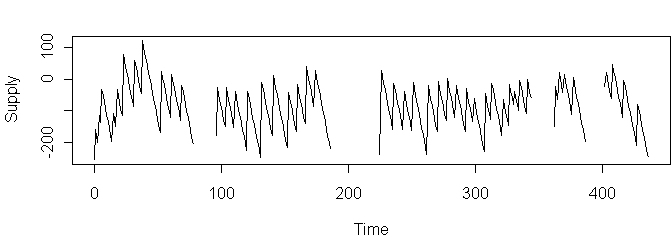
The assumption of constant consumption rate is evident in the zigzag shape.
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.471736 0.469943 -9.515 < 2e-16 ***
Supply -0.011797 0.003809 -3.097 0.00195 **
Time.since 0.220338 0.067869 3.247 0.00117 **
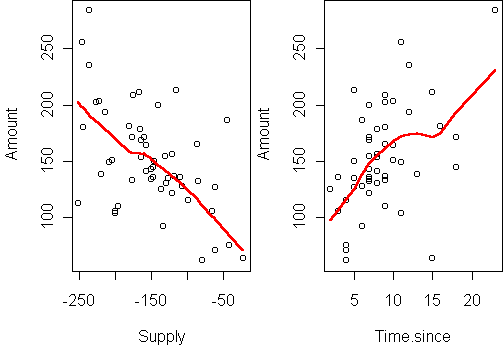
The probability of purchase depends on both time and supply,
in the expected directions: a purchase is more likely when the time since
is long and the supply is low.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 68.1482 15.0875 4.517 4.09e-05 ***
Supply -0.3915 0.1021 -3.835 0.000365 ***
Time.since 2.9479 1.3462 2.190 0.033428 *
Again the directions are intuitive. Note that supply is the most
significant predictor.
The R-squared of this fit is 42%.
So not only does the model give information about loyalty, it also gives a better fit than autoregression. The actual predictive performance, however, is unknown since the supply was estimated from the entire dataset, not just the data prior to each amount. A full treatment of this latent-variable model would estimate supply sequentially, and perhaps allow the consumption rate to change over time.
A next step would be to automate fitting the resupply model and recover coefficients for each customer, describing the extent to which their purchases depend on supply versus time, and their loyalty. This would give a map of the typical purchasing behavior for the customers of this online grocer.