Day 39 - Multivariate outliers

We've shown how projection and clustering can reveal the major ways that data points vary across a dataset. However, this is only part of the story. We are also interested in the more subtle, second-order effects, the things that make the data deviate from what we would expect on the basis of the primary effects alone. We do this by examining residuals from the primary effects.

In particular, we will look for outliers. For univariate data, outliers are easy to spot by sorting the residuals. For multivariate data, the residuals are also multivariate, so how do we define "most unusual"? One idea is to use the multivariate length of the residual: ||x - xhat||. This doesn't quite work because it doesn't consider that different variables might have different amounts of spread, and that they might be correlated.

Definition of an outlier

A better solution is to use a concept from advanced statistics called the multivariate normal distribution. It is a probability distribution defined over several variables simultaneously, e.g. (x1,x2,x3). Here is a scatterplot of a sample from a two-dimensional multivariate normal:

Like the univariate normal, there is a family of multivariate normal distributions having different means and spreads. Every member of the family is defined by the property that any linear combination of the variables is (univariate) normal. That is, a1*x1 + a2*x2 + a3*x3 is always normal, not matter what (a1,a2,a3) are. This property implies lots of things. For one, it implies that the multivariate normal density has a single peak at the mean and falls off as you move away from the mean. In other words, it is a bump, as shown in this three-dimensional plot of the two-dimensional normal sampled above:

Another implication is that the contours of the density are elliptical. Here is a contour plot of the bump, seen from above:

In general, the elliptical contours can have any shape: here they are flattened and tilted.

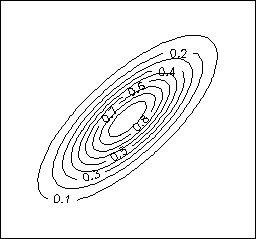
The multivariate normal distribution can be used to define outliers, just as with the univariate normal. In both cases, an outlier is a value whose probability is unexpectedly small. In the univariate case, this is a point far from the mean, in either direction. In the multivariate case, this is a point far from the mean, where some directions count more than others. Directions with large spread require the point to be farther away before it is considered an outlier.

The procedure is thus: fit a multivariate normal distribution to the dataset, compute the probability of each point, and flag the points whose probability is unexpectedly low (using p-values). The function outliers does this.

Cars

For example, on the car dataset, we find several outliers: 
> x[1,]
              Price MPG.highway EngineSize Horsepower Passengers
Acura Integra  15.9          31        1.8        140          5
              Length Wheelbase Width Turn.circle Weight
Acura Integra    177       102    68          37   2705

> i <- outliers(x)
                         D2      p.value
Chevrolet Corvette 38.21730 3.478412e-05
Mercedes-Benz 300E 34.44389 1.552920e-04
Dodge Stealth      33.78617 2.007485e-04
Mazda RX-7         32.53516 3.259493e-04
Ford Aerostar      30.49141 7.115836e-04
Geo Metro          23.73304 8.341393e-03
Chevrolet Astro    21.18824 1.981855e-02
Mercury Cougar     19.54928 3.381575e-02
Honda Civic        19.36320 3.588471e-02
Volkswagen Eurovan 18.64282 4.504106e-02
These cars all have p-values less than 5%, meaning that their probabilities are so low that we would expect a multivariate normal dataset of this size to have such cars less than 5% of the time.

For each outlier car, we would like to know what makes it different from the rest of the data: is it an unusual size, unusual price, etc.? In general, if you want to know what makes two groups different, you can think of the groups as classes and use classification methods to distinguish them. Let's use discriminative projection: 

i <- outliers(x)[1]
x$cluster <- rep(F,nrow(x))
x[i,"cluster"] <- T
x$cluster <- factor.logical(x$cluster)
sx <- scale(x)
w <- projection(sx,2,type="m")
cplot(project(sx,w),axes=F)
plot.axes(w)

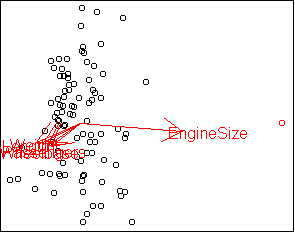
In this projection, the Corvette is clearly distinguished from other cars. The projection coefficients show that mainly this is because of its unusually large EngineSize relative to its Weight, Length, and Wheelbase. Other cars with similar Weight, Length, and Wheelbase have smaller EngineSize.

We can avoid typing the above sequence of commands by using the convenience function separate. Let's look at the second outlier car: 

> i <- outliers(x)[2]
> separate(x,i)
      Price       Width  Passengers MPG.highway   Wheelbase 
-0.84792449 -0.24664714 -0.12396093 -0.05775463 -0.02421979 
Turn.circle  EngineSize      Length      Weight  Horsepower 
 0.06843721  0.07269870  0.16373487  0.27272652  0.29957158

The projection coefficients show that the Mercedes is distinguished by a high Price relative to its Width, Weight, and Horsepower. It is a name-brand luxury car.

Finally, the third outlier car: 

> i <- outliers(x)[3]
> separate(x,i)
   Wheelbase   EngineSize        Price  Turn.circle        Width 
-0.489502780 -0.275354612 -0.195988691 -0.026335603  0.002412840 
      Length   Passengers  MPG.highway   Horsepower       Weight 
 0.015204207  0.124316064  0.194260598  0.418239977  0.645839301
The Dodge Stealth is unusual because it has the Price, EngineSize, and Wheelbase of a coupe but the Horsepower and Weight of a sports car.

States

A more refined use of this technique is to look for outliers within a cluster, since different clusters may follow a different multivariate normal distribution. Let's look at cluster 1 of the States (this is the South): 
sx <- scale(x)
hc <- hclust(dist(sx)^2,method="ward")
cluster <- factor(cutree(hc,k=4))
y <- x[cluster==1,]
> y
               Income Illiteracy Life.Exp Homocide HS.Grad Frost
Alabama          3624        2.1    69.05     15.1    41.3    20
Arkansas         3378        1.9    70.66     10.1    39.9    65
Georgia          4091        2.0    68.54     13.9    40.6    60
Kentucky         3712        1.6    70.10     10.6    38.5    95
Louisiana        3545        2.8    68.76     13.2    42.2    12
Mississippi      3098        2.4    68.09     12.5    41.0    50
New Mexico       3601        2.2    70.32      9.7    55.2   120
North Carolina   3875        1.8    69.21     11.1    38.5    80
South Carolina   3635        2.3    67.96     11.6    37.8    65
Tennessee        3821        1.7    70.11     11.0    41.8    70
Texas            4188        2.2    70.90     12.2    47.4    35
West Virginia    3617        1.4    69.48      6.7    41.6   100
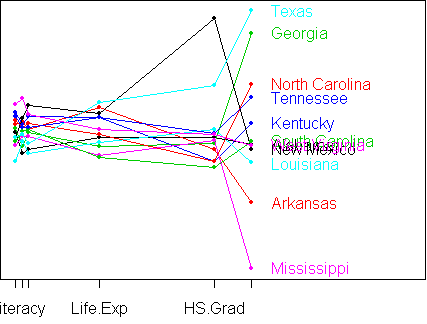
Are there any unusual states here? outliers suggests two: 
> outliers(y,0.2)
                     D2   p.value
New Mexico     9.645276 0.1404071
West Virginia  9.399917 0.1523046
Since there are only a few variables in this dataset, we can examine the outliers using a parallel-coordinate plot: 
> parallel.plot(y)
axis reversed for Illiteracy Homocide 
columns are -Illiteracy -Homocide Frost Life.Exp HS.Grad Income

New Mexico and West Virginia are adjacent on the right side. New Mexico is distinguished by having a high HS.Grad, despite mediocre values on the other dimensions. West Virgina has unusually low Illiteracy and Homocide (on the far left). Mississippi has very low Income but is not an outlier because this is not unusual given the large spread in Income across these states.

Code

Functions introduced in this lecture:
Tom Minka
Last modified: Tue Dec 04 13:18:56 Eastern Standard Time 2001