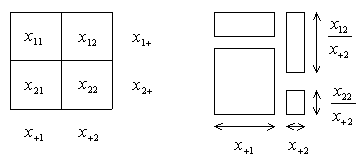
Day 12 - Visualizing contingency tables

Today we go beyond one-dimensional data and start looking at relationships between two categorical variables. Such relationships are conveniently expressed using tables of counts - contingency tables. Tables which count joint occurrences of two variables are called two-way tables.

Here is an example two-way contingency table. It reports the number of passengers on the Titanic who survived and did not survive, classified by age group:

       Survived
Age       No Yes
  Child   52  57
  Adult 1438 654

In basic statistics courses, there are only two types of contingency tables: those in which the variables are independent and those in which the variables are not independent. This decision is made via the chi-square test and summarized by a single number. For this table, there is a statistically significant dependence (the p-value is 7e-6).

In this course, we go deeper than that and try to describe the nature of the relationship between the variables. In order to do that, we will apply tools like visualization, sorting, and clustering.

Mosaic plots

A simple and effective visualization technique for contingency tables is the mosaic plot. The idea is to represent each cell by a box whose area is equal to the count in that cell. The width of the box is the same for all boxes in the same column and is equal to the total count in that column. The height of the box is the proportion of individuals in the column which fall into that cell.

Note that the mosaic treats the row and column variables differently. The column variable is treated as a conditioning variable, a "treatment", and the row variable is treated as a "response". Each column is a histogram, with bins stacked on top of each other instead of side by side.

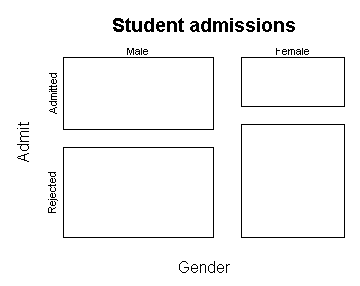
Here is the mosaic plot of the Titanic table and its transpose:

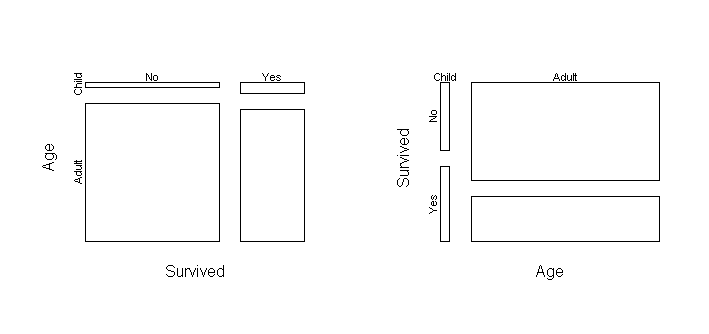
On the left plot, the height of the upper left box is the probability that someone who did not survive would be a child: p(age = child | survived = no). The width is p(survived = no). On the right plot, the height of the upper left box is the probability that a child would not be a survivor: p(survived = no | age = child). The width is p(age = child). The area of these two boxes is exactly the same, but they tell us different things. The plot on the left tells us that most of the people who survived (and did not survive) were adults, though the survivors have a greater proportion of children. The plot on the right tells us that children had a greater probability of survival than adults. It also tells us that the number of children who survived is approximately equal to the number which did not, a fact which is difficult to see in the left plot.

Stratification

Here are some more tables:

These show that women also had a greater probability of survival, as well as people in upper passenger classes.

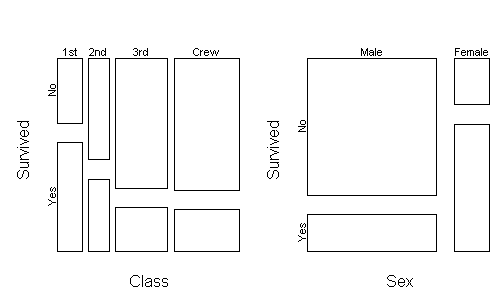
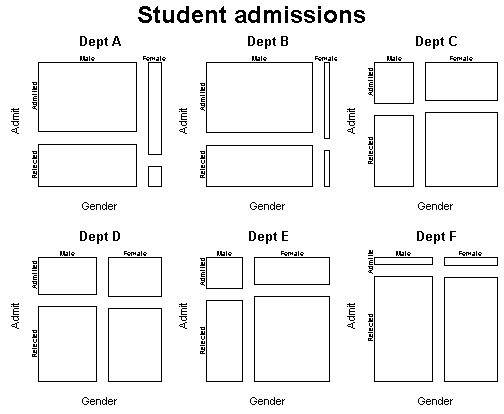
Upper classes were located higher on the ship, which may have aided their survival. Women and children were more prevalent in the upper classes, so does this explain away the sex and age effect? To answer this question, can stratify the data across class and then plot the relationship between age and survival:

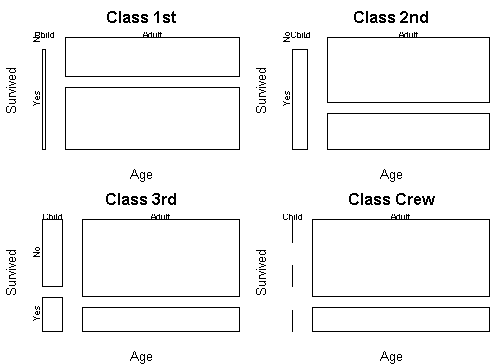
This shows that children had a higher survival rate within each class.

Independence

It is usually easy to tell from a mosaic plot whether the two variables are independent. When they are independent, all proportions are the same and so the boxes line up in a grid. This technique is illustrated on the UCBAdmissions dataset that comes with R. Here is a plot of student admissions by gender:

It seems to indicate a gender bias. However, there is a lurking variable: the department applied to. Here is what happens if we stratify on department:

It appears that most departments have no gender bias, and those departments that are biased favor women. How can this be? First, note that depts A and B have very few female applicants (the columns are narrow). It is also relatively easy to get into those departments---the proportion rejected is lower than other departments, especially F. So one explanation is that more males get in because they are applying to the hungrier, perhaps fastest-growing, departments.

Residuals

Mosaic plots represent the data as is, and do not make any attempt to generalize to the full population. To make inferences about the population, we need to provide measures of statistical significance. Inspired by the chi-square test, we can define Pearson residuals which measure the departure of each cell from independence. The formula is (actual - expected)/sqrt(expected). The units are in standard deviations, so a residual greater than 2 or less than -2 represents a departure significant at the 95% level. The expected count under independence is (row marginal)*(column marginal)/(table total).

Here is a mosaic plot, with residual shading, of hair color versus eye color in a group of statistics students (the HairEyeColor dataset in R):

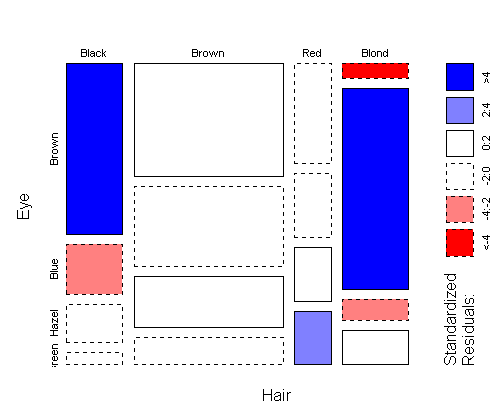
The residuals can be interpreted in the following way: a cell is shaded blue if we are confident that it is taller than the other cells in the same row. A cell is shaded red if we are confident that it is shorter than the other cells in the same row. If a cell is visibly short, but does not get shaded red, then there is not enough data to conclude that the cell would continue to be short if we took another sample. A blue cell is usually accompanied by a red cell in the same row, but not always---see e.g. the bottom row of the plot (green eyes). Note that shading does not say anything about the relative height of boxes in the same column.

For a table with lots of data, shading is redundant because all differences are significant and can be seen from the box heights. However, heights can be difficult to compare when boxes aren't lined up, as in the "hazel eyes" row. Also, shading helps draw your eye to where the major associations are.

One problem with the mosaic plot in this context is that when a proportion is very small, the corresponding box is nearly invisible and you don't see that it is colored red. Unusually large cells are emphasized in a mosaic plot, while unusually small cells are hidden.

Code

The commands we will use in this course require including the crosstab package. Download one of the following files, then type source("crosstab.r") or source("crosstab.s"), depending on your platform.

crosstab.r crosstab.s

Contingency tables are created from factor variables, using the table command. Recall that a factor is a vector of categorical observations. Here is an example:

Pet <- factor(c("Cat","Dog","Cat","Dog","Cat","Dog"))
Food <- factor(c("Dry","Dry","Dry","Wet","Wet","Dry"))
x <- table(Pet,Food)

Now x is a contingency table containing counts of each combination of a Pet category with a Food category:

     Food
Pet   Dry Wet
  Cat   2   1
  Dog   2   1

The transpose of this table is obtained via the t function, e.g. t(x):

     Pet
Food  Cat Dog
  Dry   2   2
  Wet   1   1

To save a table to disk, use write.crosstab(x,"filename"). To read it back, use read.crosstab("filename"). The table is stored in an easy-to-read format.

You can perform a classical chi-square test with chisq.test(x). The expected counts under independence can be obtained with indep.fit(x). The marginal counts can be obtained with margin.table(x,k) or equivalently apply(x,k,sum). k is a number where 1 means the row variable and 2 means the column variable.

To make a mosaicplot of a table x, say mosaicplot(x). To make a mosaicplot with residual shading, say mosaicplot(x,shade=T).

References

According to a paper by Michael Friendly, mosaic plots were originally developed by Hartigan and Kleiner in 1981. Friendly contributed the idea of residual shading in 1992. He has several papers and other resources on mosaic plots. The datasets above are frequently used in his examples.

Tom Minka

Last modified: Mon Dec 17 14:01:24 EST 2001