Semiautomatic Camera Lens Calibration
from Partially known structure

Take an image that has geometric lens distortions, where straight lines are curved

larger 55K version

My algorithm will undistort the image, straightening lines that should be straight

larger 140K version

I've corrected for lens distortion by solving for three terms of radial distortion K1, K2, K3 and two terms of decentering distortion P1, P2 where

x' = x + x*(K1*r^2 + K2*r^4 + K3*r^6) + P1*(r^2 + 2*x^2) + 2*P2*x*y
y' = y + y*(K1*r^2 + K2*r^4 + K3*r^6) + P2*(r^2 + 2*y^2) + 2*P1*x*y

In this case the estimated parameters came out to be

K1: 1.105763E-01
K2: 1.886214E-02
K3: 1.473832E-02
P1:-8.448460E-03
P2:-7.356744E-03

To solve for the 5 distortion parameters I model estimation error as vanishing point dispersion. The best estimated 5 parameters are those that minimize the weighted sum of vanishing point dispersals.

Say we make a Gaussian sphere that describes scene directions relative to an arbitrary center of projection. Each image segment is the result of projecting a scene edge thru the center of projection. Thus each scene edge lies somewhere in the plane created by the two points of an image segment and the center of projection. This plane may be described by the two sphere points on the Gaussian sphere that lie along the plane normal from the center of projection. In an undistorted image, all image segments that belong to a set of parallel lines should intersect at a common point, typically called the vanishing point. In the Gaussian sphere the sphere points of these image segments create a great circle whose plane normal points in the direction of the image vanishing point.

However, if the image is distorted (i.e. subject to lens distortion) then the set of image segments will not intersect at a common point. Similarly, the corresponding sphere points will not form a compact great circle.

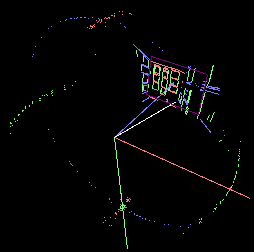
For example, here we see segments from the original distorted image. Red, green and blue line segments denote image lines that belong to scene edges that share the same scene direction.

Notice the clouds of points on the Gaussian sphere also colored red, green and blue. Each colored cloud should have sphere points which lie on a great circle whose plane normal points in the direction of the vanishing point. However, due to geometric distortion the corresponding sphere points are dispersed.

This dispersion can be measured as a sum of distances from sphere points to the great circle's plane weighted by the certainty of that line segment. When this dispersion measure is minimized (as seen below) sphere points lie much closer to their respective great circle.

Consequently image segments of the corrected image will intersect at a common vanishing point and edges which were previously warped will be straightened.

Besides having the effect of straightening curved lines (as is done by so called ``plumb-line'' methods) this approach imposes the added constraint that the projection of parallel sets of lines have a common and unique vanishing point.