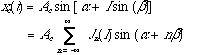3.1 A New Parameter for Frequency Modulation

Although the FM method of sound synthesis is very powerful, the degree to which the spectral envelope of a synthesized waveform can be modified or controlled is limited by the intrinsic symmetry of the envelope of the sidebands of the FM spectrum. Palamin and Palamin [1] have suggested that with a simple modification to Chowning's FM equation, i.e. equation 2.4, it is possible to easily introduce a degree of asymmetry in the sideband envelope and thereby greatly increase the control of the shape of the desired spectral envelope of the synthesized waveform.

To simplify our discussion of asymmetrical FM, let [omega]_ct = a and [omega]_mt = [beta]. Equations 2.4 and 2.13 will then become :

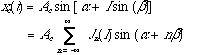(3.1)

We now introduce the new parameter r as defined by Palamin & Palamin [1]. Equation 3.1 is modified thus :

(3.2)

We note that each harmonic with maximum amplitude J_n(I) is to be multiplied by rⁿ. r is in effect the ratio of a geometric progression applied on the terms J_n(I).

The right-hand side of equation 3.2 can be expressed thus :

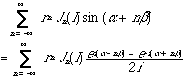(3.3)

(3.4)

where

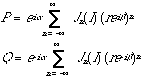(3.5)

Using the identity

(3.6)

For [gamma] = re^i[beta], x = I, we obtain

(3.7)

And for [gamma] = re^-i[beta], x = I, we obtain

(3.8)

After some mathematical manipulation, we obtain

(3.9)

If we introduce a new amplitude factor A, which is a constant, equation 3.9 will become,

(3.10)

(3.11)

where equation 3.10 is the synthesis equation and equation 3.11 is the resulting spectra.

We note that when r is set to 1.0, equations 3.10 and 3.11 will be reduced to Chowning's simple FM as in equations 2.4 and 2.13.

As can be noted from equation 3.10, the peak amplitude of the signal is amplitude modulated by an exponential function which has (I/2) (r - 1/r) multiplied by a cosine term as its argument. The exponential function will have values greater than 1. The resulting amplitude will be larger than A. If r > 1, the effect of this amplitude modulation will become very large so that the peak amplitude of the generated signal will be very large. The introduction of r has thus increased the power. It is obvious that r²ⁿ + r^-2n > 2 for any r != 1 and any n != 0, The signal can be normalized if the signal is multiplied by N = exp[-I | r - 1/r |/2]. We then have to estimate the value of the expression

(3.12)

Using the Graf addition theorem [28] and taking into account the fact that I₀(x) = J₀(ix), we obtain

(3.13)

I₀ represents the modified Bessel function of the first kind and of order 0, and should not be confused with the modulation index. Therefore, the power normalization involves the multiplication of the signal by the following factor :

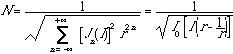(3.14)

A simpler and more efficient method of normalization includes the normalization in the synthesis process. This can be achieved by using the logarithm of the normalization factor and inserting it into the exponential waveshaping function. Then we have

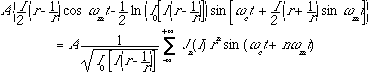(3.15)

With the normalization in equation 3.15, the generation of the synthesized waveform is stabilized and protected from excessive variation of amplitude.

By looking at equations 2.4, 2.13, 3.10 and 3.11, we can see that the AFM equation is more general than the FM equation and FM is therefore just a special case of AFM. This fact actually enables us to implement combined FM and AFM synthesis techniques easily. All we have to do is to change the parameter r to switch between the AFM and FM cases when required.

We can therefore have FM and AFM working side by side with each taking care of different parts of a spectrum which we want to synthesize. Another possibility is to have both of them interacting with each other to produce a set of spectrum lines that is impossible to produce by just FM alone or other methods. This is like stacking FM and AFM operators such that the output of AFM modulates the frequency of FM or vice versa.