Resources for the Unlimited Sensing Framework

Contents

If you use this code, please acknowledge the following papers:

Additionally, US Patent can be found here

% Code for Demo.
% Unlimited Sampling of Bandlimited Functions.
% Ayush Bhandari (ayush@alum.MIT.edu)
% The code is confidential and for collaborative purposes only.

clc
close all
clear all

set(0,'defaultlinelinewidth',2)

Overview Comment

This codes uses a moderate amount of noise added to the samples.

Empirically, this is well handled by the amplitude enfocing constraint on the residue function.

Occasionally, the reconstruction may fail.

Basic Function Definitions

% Following functions handles are defined that are useful later.
% * Fractional Part
% * Origin Centered Modulo Function
% * Rounding Function for Enforcing Amplitude Constraints
% * Pi-Bandlimited Kernel
% * Difference Order based on Dynamic Range and Sampling Rate


e = exp(1);

% Fractional Part
frac = @(x)  x-floor(x);

% Origin Centered Modulo Function
RD   = @(x,L) round(x./(2*L)).*2*L;

% Round Function
M = @(f,T) 2*T.*( frac(f./(2.*T) + 0.5) -0.5  );

% Bandlimited Kernel
K = @(x) sinc(x);

% Difference Order
DO_US = @(T,L,Bg) ceil((log(L) - log(Bg))/log(T*pi*exp(1)));

% Threshold Line
LT = @(L,ts) L.*ones(numel(ts),1);

% Phase-unwrapping
PU = @(data,L) unwrap(data.*(pi./L))./(pi/L);

Prepare Analog and Digital Signals

% Time

t  = -12:0.005:20; t = t(:);
%Ts = 1/(2*pi*e)-0.001;
Ts = 0.005/0.055;
%Ts = 0.05/0.005;


Td =  ceil(1/Ts);
locs = 1:Td:numel(t);
ts   = t(locs);

% Amplitudes of Random Bandlimited Signal
Z = rand(numel(t),1) + 1i.*rand(numel(t),1);

F = fft(K(t)).*Z;
f = real(ifft(F));
f = f./max(abs(f));
f = f-mean(f);
%f = f + 0.3.*t;

Modulo-Folded Samples

% Conventional Samples
data = f(locs);
data0 = data;

% Modulo Threshold
L     = randi([1 10],1,1)/100;
L     = 0.01 + (0.1-0.01).*rand(1,1);
L     = 1/60;

% Modulo Samples
mdata = M(f,L);

% Modulo Samples
mdm   = M(data,L);

Reconstruction from Folded Samples

% Maximum Derivative
DO  = DO_US(mean(diff(ts)),L,max(f));

% Reconstruct Initial Data
rec = M(diff(mdm,DO),L);

tsDO = ts(1:end-DO);
plot(tsDO,rec,tsDO,LT(L,tsDO),tsDO,-LT(L,tsDO));

% Reconstruction Loop
clear Kn ds res al bl

ds = diff(mdm,DO);
res = rec(:) - ds(:);
res = RD(res,L);

 cntr = cell(DO);

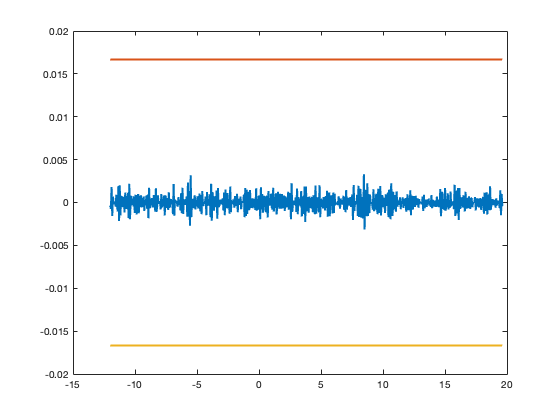
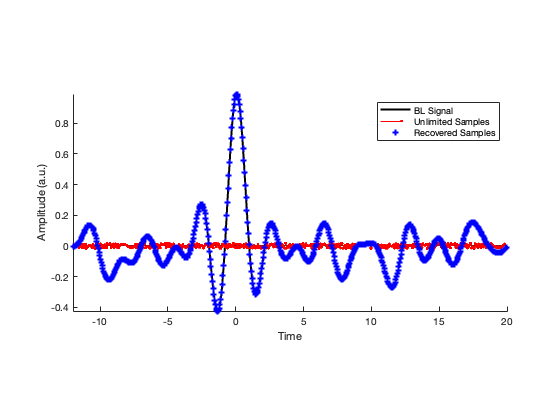
clear S2 Kn_iter Rec_Sig al bl egN cntr

al = res;                   % Initialized Variables
bl = res;                   % Initialized Variables
egN = al;                   % Initialized Variables

g0 = ceil(max(abs(data)));
Bg = ceil(g0/(2*L))*2*L;    % Ceiling of Max-norm
J =  ceil(6*Bg/L);          % Empirically This works Well


% Loop Backwards for Reconstruction
for k =  1: DO-1;
    cntr{k} = egN;
    S2 = cumsum([0 ;(cumsum([0;egN]))]);
    Kn_iter = floor((-S2(J+1) + S2(1))/(12*Bg) + 0.5)
    bl = cumsum([0; bl]);
    bl = RD(bl,L);
    bl = bl + 2*Kn_iter*L;
    egN = bl;
end

close all


Rec_Sig = cumsum([0; bl])+mdm(:);
offset = (data(locs(1)) - Rec_Sig(1))/L;
Rec_Sig = Rec_Sig + offset*L;

%Rec_Sig  = Rec_Sig - mean(Rec_Sig);

hold on;
plot(t,f,'k')
stem(ts,mdm,'r.','MarkerSize',4)
plot(ts,Rec_Sig,'b*','MarkerSize',2)
axis tight

xlabel('Time')
ylabel('Amplitude (a.u.)')
legend('BL Signal','Unlimited Samples','Recovered Samples')

pbaspect([4 2 2])

Kn_iter =

     0


Kn_iter =

     0


Kn_iter =

     0


Kn_iter =

     0


Kn_iter =

     0

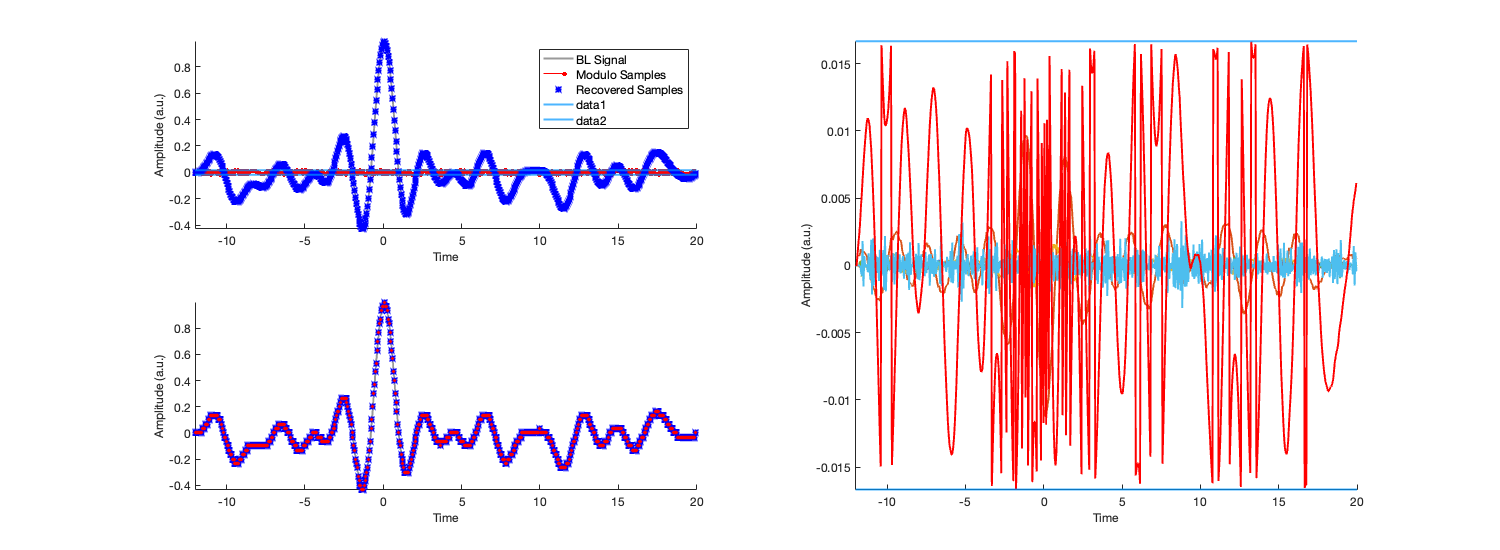
subplot(2,2,1)
hold on;
plot(t,f,'Color',[1 1 1].*0.6)
stem(ts,mdm,'Marker','.','MarkerSize',10,'MarkerFaceColor',[1 0 0],...
    'LineWidth',0.5,...
    'Color',[1 0 0])

RP = plot(ts,Rec_Sig,'b*','MarkerSize',3);



legend('BL Signal','Modulo Samples','Recovered Samples')

h1 = plot(t,-LT(L,t));
h2 = plot(t,+LT(L,t));
axis tight

h1.Color = [0 150 255]./255;
h2.Color = [0 150 255]./255;
h1.Color(4) = 0.7;
h2.Color(4) = 0.7;
RP.Color(4) = 0.2;

xlabel('Time')
ylabel('Amplitude (a.u.)')


%offset*L*0
subplot(2,2,3)
hold on;
stairs(t,f - M(f,L),'Color',[1 1 1].*0.6,'LineWidth',2)
h1 = plot(ts,cumsum([0 ; bl])+offset*L,'b*');
h1.Color(4) = 0.3;
plot(ts, data - mdm,'rsq','MarkerSize',2)
axis tight
xlim([min(t) max(t)])
xlabel('Time')
ylabel('Amplitude (a.u.)')


subplot(2,2,[2 4])
hold on;

for DO_iter = 1:DO
MDO(DO_iter,:) = [zeros(DO_iter,1);M(diff(mdm,DO_iter),L)];
end

plot(ts,MDO,ts,[0 ; M(diff(M(data,L)),L)],'r')
h1 = plot(t,-LT(L,t));
h2 = plot(t,+LT(L,t));
axis tight

h1.Color = [0 150 255]./255;
h2.Color = [0 150 255]./255;
h1.Color(4) = 0.7;
h2.Color(4) = 0.7;


axis tight
xlim([min(t) max(t)])
xlabel('Time')
ylabel('Amplitude (a.u.)')



FS = 12;
X = 600; Y = 220;
fig = gcf;
set(fig, 'Position', [0, 0, X, Y]);

fig = gcf;
set(findall(fig,'-property','FontSize'),'FontSize',FS)
set(fig, 'Position', [0, 0, X, Y].*2.5)

Report on Reconstruction

clc
disp(sprintf(['Noise Power in dB: %g'], SNR_db));
disp(sprintf(['Max-norm (Bg): %g'], Bg));
disp(sprintf(['ADC Threshold: %g'], L));
disp(sprintf(['Maximum Derivative Order: %g'], DO));
disp(sprintf(['Reconstruction MSE is %g'], immse(Rec_Sig,data)));

Unrecognized function or variable 'SNR_db'.

Error in Unlimited_Sampling_Demo (line 270)
disp(sprintf(['Noise Power in dB: %g'], SNR_db));

Published with MATLAB® R2024a